Kumar Mittal Solutions for Exercise 2: For DIFFERENT COMPETITIVE EXAMINATIONS

Light of wavelength $\lambda$ falls on a cathode plate inside a vacuum tube as shown in the figure. The work function of the cathode surface is $W$ and the anode is a wire mesh of conducting material kept at a distance $d$ from the cathode. A potential difference $V$ is maintained between the electrodes. If the minimum de-Broglie wavelength of the electrons passing through the anode is ${\lambda }_e$, which of the following statement is true?

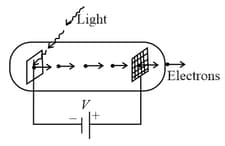
A photoelectric material having work-function $W$ is illuminated with light of wavelength $\lambda \left(\lambda <\frac{hc}{W}\right)$. The fastest photoelectron has a de-Broglie wavelength ${\lambda }_d$. A change in wavelength of the incident light $∆\lambda$ results in a change $∆{\lambda }_d$ and ${\lambda }_d$. Then the ratio $\frac{∆{\lambda }_d}{∆\lambda }$ is proportional to:

An electron of mass $m$ with an initial velocity $\overrightarrow{v}=v_0\hat{i}\left(v_0>0\right)$ enters an electric field $\overrightarrow{E}=-E_0\hat{i}\left(E_0=\mathrm{constant}>0\right)$ at $t=0$. If ${\lambda }_0$ is its de-Broglie wavelength at time $t=0$ then wavelength at time $t$ is:

Two particles move at right angle to each other. Their de-Broglie wavelengths are ${\lambda }_1$ and ${\lambda }_2$ respectively. The particles suffer perfectly inelastic collision. The de-Broglie wavelength $\lambda$, of the final particle, is given by:

A particle $\text{'}P\text{'}$ is formed due to  completely inelastic collision of particles $\text{'}x\text{'}$ and $\text{'}y\text{'}$ having de-Broglie wavelengths $\text{'}{\lambda }_x\text{'}$ and $\text{'}{\lambda }_y\text{'}$ respectively. If $x$ and $y$ were moving in opposite directions, then the de-Broglie wavelength of $\text{'}P\text{'}$ is:

An electron is accelerated through a potential difference of $10000 \mathrm{V}$. Its de-Broglie wavelength is, (nearly): $\left(m_e=9\times {10}^{-31} \mathrm{kg}\right)$.

A nucleus $A$, with a finite de-Broglie wavelength ${\lambda }_A$, undergoes spontaneous fission into two nuclei $B$ and $C$ of equal mass. $B$ flies in the same direction as that of $A$, while $C$ flies in the opposite direction with a velocity equal to half of that of $B$. The de-Broglie wavelengths ${\lambda }_B$ and ${\lambda }_C$ of $B$ and $C$ are respectively:

If the de-Broglie wavelength of an electron is equal to ${10}^{-3}$ times the wavelength of a photon of frequency $6\times {10}^{14} \mathrm{Hz}$, then the speed of the electron is equal to: (Speed of light$=3\times {10}^8 \mathrm{m}/\mathrm{s}$, Plank's constant$=6.63\times {10}^{-34} \mathrm{J}-\mathrm{s}$, Mass of electron$=9.1\times {10}^{-31} \mathrm{kg}$).