Exercise 9.1

The angle of elevation of the top of a building from the foot of the tower is $\mathrm{}{30}^{\mathrm{o}}$ and the angle of elevation of the top of the tower from the foot of the building is $60°$. If the tower is $50 \mathrm{m}$ high, find the height of the building.

Two poles of equal heights are standing opposite each other on either side of the road, which is $80 \mathrm{m}$ wide. From a point between them on the road, the angles of elevation of the top of the poles are $60°$ and $30°$, respectively. Find the height of the poles and the distances of the point from the poles.

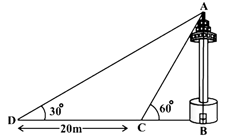
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is $60°$. From another point $20 \mathrm{m}$ away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is $30°$. Find the height of the tower and the width of the canal.

From the top of a $7 \mathrm{m}$ high building, the angle of elevation of the top of a cable tower is $60°$ and the angle of depression of its foot is $45°$. Determine the height of the tower.

As observed from the top of a $75 \mathrm{m}$ high lighthouse from the sea-level, the angles of depression of two ships are $30°$ and $45°$. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.

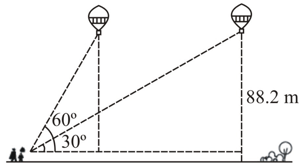
A $1.2 \mathrm{m}$ tall girl spots a balloon moving with the wind in a horizontal line at a height of $88.2 \mathrm{m}$ from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is $60°$. After some time, the angle of elevation reduces to $30°$ (see Fig.). Find the distance travelled by the balloon during the interval.

A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of $\mathrm{}{30}^{\mathrm{o}}$, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be $\mathrm{}{60}^{\mathrm{o}}$.

Find the time taken by the car to reach the foot of the tower from this point.

The angles of elevation of the top of a tower from two points at a distance of $4 \mathrm{m}$ and $9 \mathrm{m}$ from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is $6 \mathrm{m}$.