Telangana Board Solutions for Chapter: Similar Triangles, Exercise 9: Exercise

$\text{'}O\text{'}$ is any point in the interior of a triangle $\text{ABC}.$
If $\mathrm{OD}\perp \mathrm{BC}, \mathrm{OE}\perp \mathrm{AC}$ and $OF\perp \mathrm{AB}$ show that
${\mathrm{AF}}^2+{\mathrm{BD}}^2+{\mathrm{CE}}^2={\mathrm{AE}}^2+{\mathrm{CD}}^2+{\mathrm{BF}}^2$

A wire attached to a vertical pole of height $18 \mathrm{m}$ is $24 \mathrm{m}$ long and has a stake attached to the other end. If the stake be driven $d \mathrm{m}$ from the base of the pole, so that the wire will be taut, then what is the value of $d$ (correct to one decimal place)? [Take $\sqrt{7}=2.64$]

Two poles of heights $6 \mathrm{m}$ and $11 \mathrm{m}$ stand on a plane ground. If the distance between the feet of the poles is $12 \mathrm{m}$ and the distance between their tops is $d \mathrm{m}$, then find the value of $d$.

In an equilateral triangle $ABC\mathit{,}\mathit{ }D$ is a point on side $BC$ such that $BD=\frac{1}{3}BC$. Prove that $9A{D}^2=7A{B}^2$

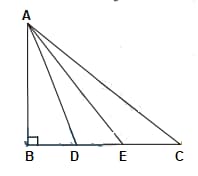
In the given figure, $ABC$ is a triangle right-angled at $B. D$ and $E$ are points on $BC$ trisect it.
Prove that $8{\mathrm{AE}}^2=3{\mathrm{AC}}^2+5{\mathrm{AD}}^2$

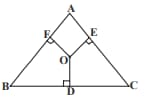
$\mathrm{ABC}$ is an isosceles triangle right angled at $\text{B}.$ Similar triangles $\text{ACD}$ and $\text{ABE}$ are constructed on sides $\text{AC}$ and $\text{AB}.$ Find the ratio between the areas of $∆\text{ABE}$ and $∆ \text{ACD}$.

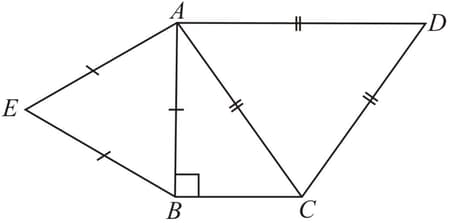
Equilateral triangles are drawn on the three sides of a right-angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangles described on its diagonal.