Embibe Experts Solutions for Chapter: Linear Programming, Exercise 1: Exercise

The feasible region for an $\mathrm{LPP}$ is shown in the figure. Let $F=3x-4y$ be the objective function.

The minimum value of $F$ is

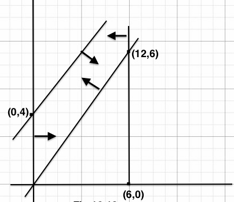
If the objective function is $Z =6x-7y$. Identify the decision variables

A factory uses three different resources for the manufacture of two different products, $20$ units of the resource $A$, $12$ units of $B$ and $16$ units of $C$ being available. One unit of the first product requires $2, 2$ and $4$ units of the resources and one unit of the second product requires $4, 2$ and $0$ units of the resources taken in order. It is known that the first product gives the profit of $₹20$ per unit and the second $₹30$ per unit. Formulate the LPP so as to earn maximum profit.

If the objective function is $Z =ax+by$. Identify the decision variables

A company manufactures and sells two models of lamps $L_1$ and $L_2$, the profit being $₹15$ and $₹10$ respectively. The process involves two workers $W_1$ and $W_2$ who are available for this kind of work $100$ hours and $80$ hours per month respectively, $W_1$ assembles $L_1$ in $20$ and $L_2$ in $30$ minutes. $W_2$ paints $L_1$ in $20$ and $L_2$ in $10$ minutes. Assuming that all lamps made can be sold, formulate LPP for determining the productions figures for maximum profit.

If the objective function is $Z =10x+7y$. Identify the decision variables

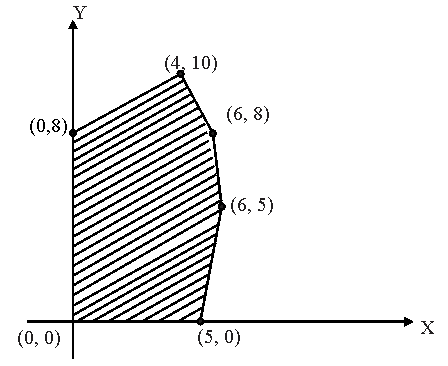
The feasible solution for a Linear Programming Problem is shown in Figure. Let $Z=3x-4y$ be the objective function. Minimum of $Z$ occurs at

If a man drives his vehicle at $25 \mathrm{km}/\mathrm{hr}$, he has to spend $\mathrm{Rs}. 4 \mathrm{per} \mathrm{km}$. on petrol. If he drives it at a faster speed of $80 \mathrm{km}/\mathrm{hr}$. the petrol cost increases to $\mathrm{Rs}. 7.5 \mathrm{per} \mathrm{km}$. He has $\mathrm{Rs}. 800$ to spend on petrol and travel within $2$ hours. How many hours should he move in the given two speeds so as to make the distance travelled maximum? Formulate the problem as an LPP and then solve graphically.