Embibe Experts Solutions for Chapter: Some Applications of Trigonometry, Exercise 1: Exercise

The angle of depression from the top of a vertical tower to a point on the ground is found to be 60° and from a point 50m above the foot of the tower the angle of depression to the same point is found to be 30⁰ as shown in the figure find the height of the tower.

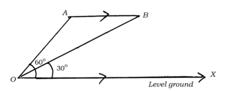
An aircraft flying parallel to the ground in the sky from the point $A$ through the point $B$ is observed, the angle of elevation of aircraft at $A$ from a point on the level ground is $60°$, after $10$ seconds it is observed that the angle of elevation of aircraft at $B$ is found to be $30°$ from the same point. Find at what height the aircraft is flying, if the velocity of aircraft is $648 \mathrm{km}/\mathrm{hr}$.

(Use $\sqrt{3}=1.73$)

The angles of elevation of the top of a tower from two points at a distance of $4 m \&\hspace{0.17em}9 m$ from the base of the tower and in the same straight line with it are complementary. If the height of the tower is $k m$, then find the value of $k$.

A coast guard attendant atop a cliff $120 \mathrm{m}$ high observes two boats in line with him at angles of depression of $45$ degrees and $69$ degrees. Determine how far apart the boats are.

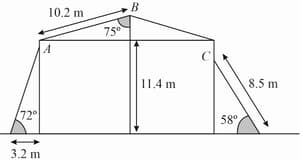
Find the heights from the ground of $A, B$ and $C$.

A vertical stick $1 \mathrm{m}$ long casts a shadow which is $1.3 \mathrm{m}$ long. Determine the altitude of the sun (its angle of elevation).

Gina is flying a kite that makes a $50°$ angle with the ground. Determine how high the kite is above the ground when she has let out $150 \mathrm{m}$ of string.

From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be $\alpha$ and $\beta .$ Show that the height (in miles) of aeroplane above the road is given by $\frac{\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }$.