Embibe Experts Solutions for Chapter: Surface Areas and Volumes, Exercise 1: Exercise

A storage bin is in the shape of a frustum of a pyramid whose bases are parallel rectangles. The upper base is $4 \mathrm{m}$ by $6 \mathrm{m}$ and the lower base is $2 \mathrm{m}$ by $3 \mathrm{m}$. If its capacity is $65 \mathrm{cu}. \mathrm{m}.$, what is the depth of the bin?

Jumbo circus team is a very famous circus company in south India. They roam around in the different parts of the counts and host the circus treat for the people. When they are settling at a place, they will erect their huge circus tent for performing the show and small tents for them to stay in those days. The stage tent consists of a cylinder capped by a cone.

The height and radius of the base of a conical portion is $21$ metre and $28$ metre. The lower part of a tent is in the form of a right circular cylinder whose height is $32.5$ metre. What will be the diameter of the cylinder and the total height of the tent?

What is the lateral area of a frustum of a regular square pyramid of $20 \mathrm{cm}$ and $10 \mathrm{cm}$ sides of the lower and upper bases and an altitude of $40 \mathrm{cm}$?

The volume of the frustum of a regular triangular pyramid is $135 \mathrm{cu}. \mathrm{m}.$. The lower base is an equilateral triangle with an edge of $9 \mathrm{m}$ The upper base is $8 \mathrm{m}$ above the lower base. What is the upper base edge in meters?

The bases of a frustum of a square pyramid are of lengths $9$ units and $6$ units. Its slant height is $10$ units. Find the total surface area of frustum of the pyramid

Find the volume of a frustum of a regular pyramid whose area of bases are $40 {\mathrm{cm}}^2$, $25 {\mathrm{cm}}^2$ respectively and height is $10 \mathrm{cm}$.

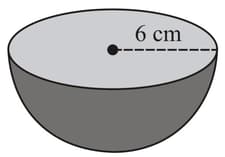
Calculate the surface area of the following solid.

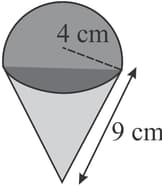
Find the volume of the following $3D$ solid.