H K Dass, Rama Verma and, Bhagwat Swarup Sharma Solutions for Chapter: Co-Ordinate Geometry, Exercise 5: REVISION EXERCISE

If the points $(1, 4), (r, -2)$ and $(-3, 16)$ are collinear, find the value of $\text{'}r\text{'}$.

If $A(3, 0), B(4, 5), C(-1, 4)$ and $D(-2, -1)$ be four points in a plane, show that $ABCD$ is a rhombus but not a square.

The base $BC$ of an equilateral triangle $ABC$ lies on $y-$axis. The coordinates of the point $C$ are $(0,-3)$. If the origin is the midpoint of $BC$, find the coordinates of points $A$ and $B$.

Show that the points $(7, 3), (3, 0), (0, -4)$ and $(4, -1)$ are the vertices of a rhombus.

The area of a triangle $ABC$ is $k {\mathrm{cm}}^2$, whose vertices (in $\mathrm{cm}$) are $A\left(4, 4\right), B\left(0, 0\right)$ and $C\left(6, 2\right)$. Now, find the value of $k$? 

In $∆ABC$, $D$ and $E$ are the midpoints of the sides $BC$ and $AC$, respectively. Find the length of $DE$. Prove that $DE=\frac{1}{2}AB$.

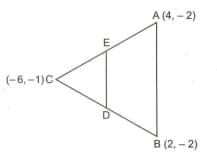
Show that the points $\left(-4, 0\right), \left(4, 0\right)$ and $\left(0, 3\right)$ are the vertices of an isosceles triangle.

Find the area (in sq. unit) of the triangle formed by joining midpoints of the sides of the triangle whose vertices are $\left(0, -1\right), \left(2, 1\right)$ and $\left(0, 3\right)$.