B M Sharma Solutions for Chapter: Basic Mathematics, Exercise 70: CONCEPT APPLICATION EXERCISE 2.7

The speed of a car increases uniformly from zero to $10 \mathrm{m} {\mathrm{s}}^{-1}$ in $2 \mathrm{s}$ and then remains constant (figure).

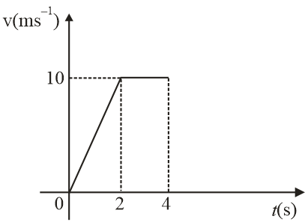
(a) Find the distance travelled by the car in the first $2 \mathrm{s}$.

(b) Find the distance travelled by the car in the next $2 \mathrm{s}$.

(c) Find the total distance travelled in $4 \mathrm{s}$.

A car accelerates from rest with $2 \mathrm{m} {\mathrm{s}}^{-2}$ for $2 \mathrm{s}$ and then decelerates constantly with $4 \mathrm{m} {\mathrm{s}}^{-2}$ for $t_0$ second to come to rest. The graph for the motion is shown in figure.

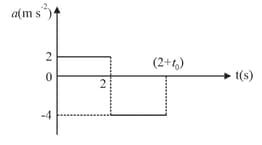
(a) Find the maximum speed attained by the car.

(b) Find the value of $t_{0_{}}$.

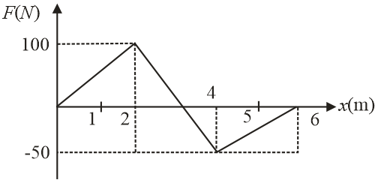
A stationary particle of mass $m=1.5 \mathrm{kg}$ is acted upon by variable force. The variation of force with respect to displacement is plotted in the figure below.

(a) Calculate the velocity acquired by the particle after getting displaced through $6 \mathrm{m}$.

(b) What is the maximum speed attained by the particle and at what time is it attained?

The displacement of a body at any time $t$ after starting is given by $s=15t-0.4t^2$. Find the time when the velocity of the body will be $7 \mathrm{m} {\mathrm{s}}^{-1}$.

A particle moves along a straight line such that its displacement at any time $t$ is given by $s=t^3-6t^2+3t+4 \mathrm{m}$. Find the velocity when the acceleration is $0$.

The displacement $x$ of a particle moving in one dimension under the action of a constant force is related to time $t$ by the equation $t=\sqrt{x}+3$, where $x$ is in $\mathrm{meter}$ and $t$ is in $\mathrm{second}$. Find the displacement of the particle when its velocity is zero.

The acceleration of a motorcycle is given by $a_{\mathrm{x}}\left(t\right)=At-B{t}^2$, where $A=1.50 \mathrm{m} {\mathrm{s}}^{-3}$ and  $B=0.120 \mathrm{m} {\mathrm{s}}^{-4}$. The motorcycle is at rest at the origin at time $t=0$.

(a) Find its position and velocity as functions of time.

(b) Calculate the maximum velocity it attains.

The acceleration of a particle varies with time $t$ seconds according to the relation $a=6t+6 \mathrm{m} {\mathrm{s}}^{-2}$. Find velocity and position as functions of time. It is given that the particle starts from origin at $t=0$ with velocity $2 \mathrm{m} {\mathrm{s}}^{-1}$.