B M Sharma Solutions for Chapter: Circular Motion, Exercise 56: Exercises

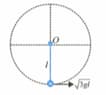
A particle of mass $5 \mathrm{kg}$ is free to slide on a smooth ring of radius $r=20 \mathrm{cm}$ fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point $O$ of the ring. Initially, the particle is at rest at a point $A$ of the ring such that $\angle OCA=60°\text{,} C$ being the centre of the ring. The natural length of the spring is also equal to $r=20 \mathrm{cm}$. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position $B$. The force constant is given as 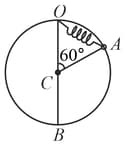$x\times {10}^2 \mathrm{N} {\mathrm{m}}^{-1}$

Find the value of $x$

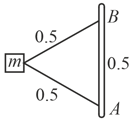
Two strings of lengths, $l=0.5 \mathrm{m}$ each are connected to a block of mass, $m=2 \mathrm{kg}$ at one end and their ends are attached to the point $A$ and $B\text{,} 0.5 \mathrm{m}$ apart on a vertical pole which rotates with a constant angular velocity, $\omega =7 \mathrm{rad} {\mathrm{s}}^{-1}$. Find the ratio $\frac{T_1}{T_2}$ of tension in the upper string $\left(T_1\right)$ and the lower string $\left(T_2\right)$. [Use, $g=9.8 \mathrm{m} {\mathrm{s}}^{-2}$.]

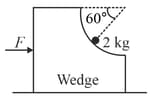
A wedge is placed on a smooth horizontal surface. It contains a circular quadrant of radius $25 \mathrm{cm}$ as shown. An insect crawls on the circular part with a constant speed $0.5 \mathrm{m} {\mathrm{s}}^{-1}$. A force $F$ is applied on the wedge so that it does not move. Find the value of $F$ in newton when radial line of position of insect makes an angle of $60°$ with horizontal.

A force of constant magnitude, $F=10 \mathrm{N}$ acts on a particle moving in a plane such that it is perpendicular to the velocity $\overrightarrow{v}\left(\left|\overrightarrow{v}\right|=v=5 \mathrm{m} {\mathrm{s}}^{-1}\right)$ of the body and the force is always directed towards a fixed point. Then, the angle (in radian) turned by the velocity vector of the particle as it covers a distance, $S=10 \mathrm{m}$ is (take the mass of the particle as, $m=2 \mathrm{kg}$),

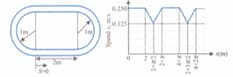
A toy car is moving anticlockwise on a closed track whose curved portions are semicircles of radius $1 \mathrm{m}$. The adjacent graph describes the variation of speed of the car with distance moved by it (starting from point $S$). Find the time $\left(t\right)$ required for the car to complete one lap in second, (take   $\pi \ln \left(2\right)\approx 2$)

Small parts each of mass $m$ on a conveyer belt moving with constant velocity are allowed to drop into a bin. Radius of circular portion is $2 \mathrm{m}$. The static coefficient of friction between the parts and belt ${\mu }_s$ is $1$. If the parts start sliding on the belt at the angle $\alpha ={37}^{\mathrm{o}}$. Find the velocity (in ${\mathrm{ms}}^{-1}$) of conveyer belt.

One end of a massless spring of spring constant $100 {\mathrm{Nm}}^{-1}$ and natural length $0.5 \mathrm{m}$ is fixed and the other end is connected to a particle of mass $0.5 \mathrm{kg}$ lying on a frictionless horizontal table. The spring remains horizontal. If the mass is made to rotate at an angular velocity of $2 {\mathrm{rads}}^{-1}$, find the elongation of the spring (in $\mathrm{cm}$).

A ball is given a velocity of $\sqrt{3gl}$ as shown. If the ratio of centripetal acceleration to tangential acceleration is $1: y\sqrt{2}$ at the point where the ball leaves circular path then write the value of $y$. [Neglect the size of ball]