B M Sharma Solutions for Chapter: Electric Potential, Exercise 1: Concept Application Exercise
B M Sharma Physics Solutions for Exercise - B M Sharma Solutions for Chapter: Electric Potential, Exercise 1: Concept Application Exercise
Attempt the free practice questions on Chapter 3: Electric Potential, Exercise 1: Concept Application Exercise with hints and solutions to strengthen your understanding. PHYSICS for Joint Entrance Examination JEE (Advanced) Electrostatics and Current Electricity solutions are prepared by Experienced Embibe Experts.
Questions from B M Sharma Solutions for Chapter: Electric Potential, Exercise 1: Concept Application Exercise with Hints & Solutions
Find out the following :
a)
b)
c)
d)
e)
f) Arrange the order of potential for points .
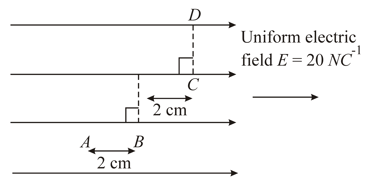
Find potential difference between points in an electric field , where and .
At a point due to a point charge, the values of electric field intensity and potential are and respectively. Calculate the magnitude of the charge and calculate the distance of the charge from the point of observation.
Two uniformly charged large plane sheets and having charge densities and are placed at a distance parallel to each other. A charge is moved along a line of length at an angle with the normal to . Calculate the work done by the electric field.
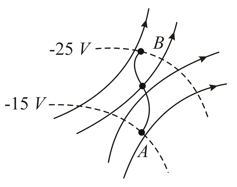
The figure shows field lines and equipotential (dashed) lines.
(a) Find the external work done to move a charge at constant speed from to along the path shown.
(b) Find the work done by the electric field.
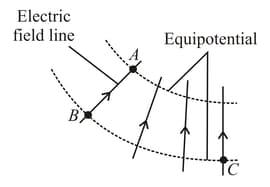
In moving from to along an electric field, the electric field does of work on an electron in the field illustrated in the figure. What are the differences in the electric potential? Find the potential difference a) b) c)
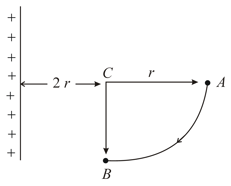
A charge is transported from point to along the arc with centre at as shown in the figure near a long charged wire with linear density lying in the same plane. Find the work done by the external agent in doing so.
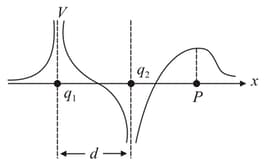
The graphical variation of electric potential due to point charge and lies on the -axis at some separation , which is shown in the figure. If the origin is the point between the charges where potential is zero. Distance of from origin is . Find the distance of point (marked in the figure) from charge .