B M Sharma Solutions for Chapter: Electric Potential, Exercise 4: Concept Application Exercise

Water from a tap, maintained at a constant potential $V$, is allowed to fall by drops of radius $r$ through a small hole into a hollow conducting sphere of radius $R$ standing on an insulating stand until it fills the entire sphere. Find the potential of the hollow conductor after it is completely filled with water.

Two identical thin rings, each of radius $R \mathrm{m}$, coaxially placed at a distance $R \mathrm{m}$ from each other. If $Q_1$ coulomb and $Q_2$ coulomb are the charges uniformly spread on the two rings, find the work done in moving a charge $q$ from the center of one ring to that of the other.

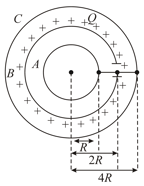
Three conducting spherical shells have radii $a, b$ and  $c$ such that $a<b<c$ (figure). Initially, the inner shell is uncharged, the middle shell has a positive charge $Q$, and the outer shell has a negative charge $-Q$.

(a) Find the electric potential of the three shells.

(b) If the inner and outer shells are now connected by a wire that is insulated as it passes through the middle shell, what is the electric potential of each of the three shells? Also, what is the final charge on each shell?

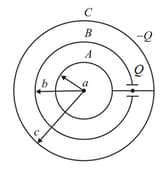
The figure shows three concentric spherical conductors $A, B, C$ with radii $R, 2R$ and $4R$ respectively. $A$ and $C$ are connected by a conducting wire, and $B$ is uniformly charged (charge = $+Q$). Find charges on conductors $A$ and $C$ and potentials of $A$ and $B$.

A point charge $q$ is located at the center $O$ of an uncharged spherical capacitor provided with a small orifice. The inside and outside radii of capacitor are $a$ and $b$, respectively (figure). What amount of work has to be performed to slowly transfer the charge $q$ bit by bit from the point $O$ through the orifice to infinity?

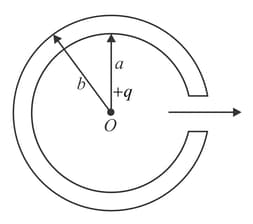
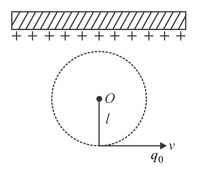
Figure shows a large conducting ceiling having uniform charge density $\sigma$ below which a charge particle of charge $q_0$ and mass $m$ is hung from point $O$, through a small string of length $l$. Calculate the minimum horizontal velocity $v$ required for the string to become horizontal.

A small ball of mass $2\times {10}^{-3} \mathrm{kg}$, having a charge $1 \mathrm{\mu C}$, is suspended by a string of length $0.8 \mathrm{m}$. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution.

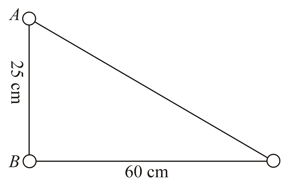
$\mathrm{ABC}$ is a right-angled triangle where $\mathrm{AB}$ and $\mathrm{BC}$ are $25 \mathrm{cm}$ and $60 \mathrm{cm}$, respectively. A metal sphere of $2 \mathrm{cm}$ radius, charged to a potential of $9\times {10}^5 \mathrm{V}$, is placed at $\mathrm{B}$. Find the amount of work done in carrying a positive charge of $1 \mathrm{C}$ from $\mathrm{C}$ to $\mathrm{A}$.