Embibe Experts Solutions for Chapter: Rotational Mechanics, Exercise 1: Exercise 1

A body whose moment of inertia is $3 \mathrm{kg} {\mathrm{m}}^2$ is at rest. It is rotated for $20 \mathrm{s}$ by a torque of $6 \mathrm{N} \mathrm{m}$, angular displacement of the body will be

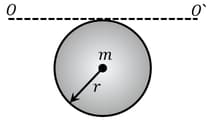
The velocity of the centre of mass of a solid sphere of radius $R$ rotating with angular velocity $\omega$ about an axis passing through its centre of mass is

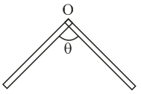
A thin rod of length $L$ and mass $M$ is bent at the middle point $O$ as shown in the figure. Consider an axis passing through two middle the point $O$ and perpendicular to the plane of the bent rod. Then the moment of inertia about this axis is

The moment of inertia of a disc about axis $O$$O\text{'}$ is $Nm{r}^2$. Axis is in the plane of disc and tangential. Then the value of $N$ is:

The moment of inertia of a metre scale of mass $0.6 \mathrm{kg}$ about an axis perpendicular to the scale and located at the $20 \mathrm{cm}$ position on the scale is $n$ $\mathrm{kg} m^2$ (Breadth of the scale is negligible). The value of $n$ is

A rod of length $L$ can rotate about end $0 .$ What is the work done if the rod is rotated by $180°$

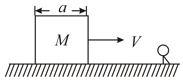
A cubical block of side a is moving with velocity $v$ on a horizontal smooth plane, as shown It hits a ridge at point $\mathrm{O}$O. The angular speed of the block after it hits $\mathrm{O}$ is

The moments of inertia of two rotating bodies $A$ and $B$ are $I_A$ and $I_B\left(I_A>I_B\right)$ and their angular momentum are equal. If their kinetic energies be $K_A$ and $K_d,$ respectively, then