B M Sharma Solutions for Chapter: Gravitation, Exercise 2: CONCEPT APPLICATION EXERCISE
B M Sharma Physics Solutions for Exercise - B M Sharma Solutions for Chapter: Gravitation, Exercise 2: CONCEPT APPLICATION EXERCISE
Attempt the practice questions on Chapter 5: Gravitation, Exercise 2: CONCEPT APPLICATION EXERCISE with hints and solutions to strengthen your understanding. Physics For Joint Entrance Examination JEE (Advanced): Mechanics II solutions are prepared by Experienced Embibe Experts.
Questions from B M Sharma Solutions for Chapter: Gravitation, Exercise 2: CONCEPT APPLICATION EXERCISE with Hints & Solutions
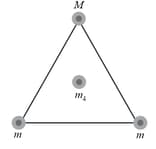
As seen in the figure shown below, two spheres of mass and a third sphere of mass form an equilateral triangle and the fourth sphere of mass is at the centre of the triangle. The net gravitational force on that central sphere from the three other spheres is zero.
(a) What is in terms of ?
(b) If we double the value of then what is the magnitude of the net gravitational force on the central sphere?
Three identical particles, each of mass , are located in space at the vertices of an equilateral triangle of side length . They are revolving in a circular orbital under mutual gravitational attraction. Find the speed of each particle.
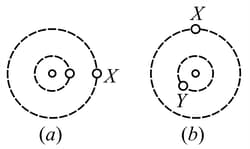
Two planets and travel counterclockwise in circular orbits about a star as shown in figure. The radii of their orbits are in the ratio . At one moment, they are aligned as shown in Fig. (a), making a straight line with the star. During the next five years, the angular displacement of planet is as shown in Fig. (b). What is the angular displacement of planet at this moment?
A thin rod with mass is bent in a scmicirclc of radius (figure).
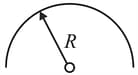
(a) What is its gravitational force (both magnitude and direction on a particle with mass at , the center of curvature?
(b) What would be the force on the particle if the rod were a complete circle?
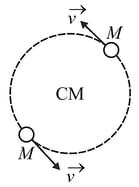
A binary system consists of two stars that revolve in a circular orbit about a center of mass midway between them. This statement implies that the masses of the two stars are equal (figure). Assume the orbital speed of each star is and the orbital period of each is days. Find the mass of each star.
Three identical points of mass each are kept at the vertices , and of a cube having side length ' ' (see figure). Another identical mass is placed at the center point of the cube.
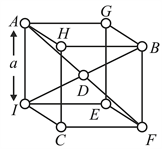
(a) Where will you place a fifth identical mass so that the net gravitational force acting on mass at becomes zero?
(b) Calculate the net gravitational force acting on the mass at .
In the figure shown below, a spherical hollow inside a lead sphere of radius the surface of the hollow passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was . With what gravitational force does the hollowed-out lead sphere attract a small sphere of mass that lies at a distance from the centre of the lead sphere, on the straight line connecting the centres of the spheres and of the hollow?

Two small balls of masses and are placed at a separation . A third ball of mass is placed at an unknown location on the line joining the first two balls such that the net gravitational force experienced by the first ball is . What is the location of the third ball?
