I E Irodov Solutions for Chapter: ELECTRODYNAMICS, Exercise 5: CONSTANT MAGNETIC FIELD, MAGNETICS

Inside a long straight uniform wire of round cross-section, there is a long round cylindrical cavity, whose axis is parallel to the axis of the wire and displaced from the latter by a distance $l$. A direct current of density $\overrightarrow{j}$ flows along the wire. Find the magnetic induction inside the cavity. Consider, in particular, the case $l=0$.

Find the current density, as a function of distance $r$ from the axis of a radially symmetrical parallel stream of electrons, if the magnetic induction inside the stream varies as $B=b{r}^{\alpha }$, where $b$ and $\alpha$ are positive constants.

A single-layer coil (solenoid) has length $l$ and cross-section radius $R$. The number of turns per unit length is equal to $n$. Find the magnetic induction at the centre of the coil, when a current $I$ flows through it.

A very long straight solenoid has a cross-section radius $R$ and $n$ turns per unit length. A direct current $I$ flows through the solenoid. Suppose that, $x$ is the distance from the end of the solenoid, measured along its axis. Find:
(a) the magnetic induction $B$, on the axis, as a function of $x$; draw an approximate plot of $B$ versus the ratio $\frac{x}{R}$;
(b) the distance $x_0$, to the point on the axis at which the value of $B$ differs by $\eta =1\%$ from that in the middle section of the solenoid.

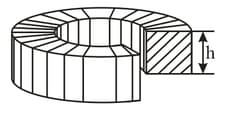
The figure shows a toroidal solenoid, whose cross-section is rectangular. Find the magnetic flux through this cross-section, if the current through the winding equals $I=1.7 \mathrm{A}$, the total number of turns is $N=1000$, the ratio of the outside diameter to the inside one is $\eta =1.6$ and the height is equal to $h=5.0 \mathrm{cm}$. 

Find the magnetic moment of a thin round loop with current, if the radius of the loop is equal to $R=100 \mathrm{mm}$ and the magnetic induction at its centre is equal to $\overrightarrow{B}=6.0$ $\mathrm{\mu T}$.

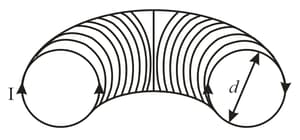
Calculate the magnetic moment of a thin wire with a current, $I=0.8 \mathrm{A}$, wound tightly on half a tore. The diameter of the cross-section of the tore, $d=5.0 \mathrm{cm}$, the number of turns is $N=500$.

A thin insulated wire forms a plane spiral of $N=100$ tight turns carrying a current, $I=8 \mathrm{mA}$. The radii of inside and outside turns are $a=50 \mathrm{mm}$ and $b=100 \mathrm{mm}$. Find, 
$\left(a\right)$ the magnetic induction at the centre of the spiral, 
$\left(b\right)$ the magnetic moment of the spiral with a given current.