I E Irodov Solutions for Chapter: PHYSICAL FUNDAMENTALS OF MECHANICS, Exercise 1: KINEMATICS

A solid body rotates with deceleration about a stationary axis with an angular deceleration $\beta \propto \sqrt{\omega }$, where $\omega$ is its angular velocity. Find the mean angular velocity of the body averaged over the whole time of rotation if at the initial moment of time its angular velocity was equal to ${\omega }_0$.

A solid body rotates about a stationary axis so that its angular velocity depends on the rotation angle $\mathrm{\phi }$ as $\omega ={\omega }_0-a\phi$, where ${\omega }_0$ and $a$ are positive constants. At the moment $t=0$ the angle $\phi =0$. Find the time dependence of
$\left(a\right)$ the rotation angle, 
$\left(b\right)$ the angular velocity.

A solid body starts rotating about a stationary axis with an angular acceleration $\overrightarrow{\beta }=\overrightarrow{{\beta }_{0 }}\cos \phi$, where $\overrightarrow{{\beta }_0}$ is a constant vector and $\mathrm{\phi }$ is an angle of rotation from the initial position. Find the angular velocity of the body as a function of the angle $\mathrm{\phi }$. Draw the plot of this dependence.

A rotating disc moves in the positive direction of the $x$-axis. Find the equation $y\left(x\right)$ describing the position of the instantaneous axis of rotation, if at the initial moment the axis $C$ of the disc was located at the point $O$ after which it moved
$\left(a\right)$ with a constant velocity $v$, while the disc started rotating counterclockwise with a constant angular acceleration $\mathrm{\beta }$ (the initial angular velocity is equal to zero),

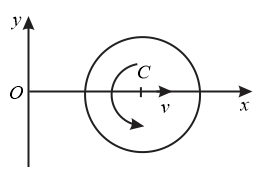
$\left(b\right)$ with a constant acceleration $w$ (and the zero initial velocity), while the disc rotates counterclockwise with a constant angular velocity $\omega$.

A point $A$ is located on the rim of a wheel of radius $R=0.50 \mathrm{m}$ which rolls without slipping along a horizontal surface with velocity $v=1.00 \mathrm{m} {\mathrm{s}}^{-1}$. Find, 
$\left(a\right)$ the modulus and the direction of the acceleration vector of the point $A$, 
$\left(b\right)$ the total distance $s$ traversed by the point $A$ between the two successive moments at which it touches the surface.

A ball of radius $R=10.0 \mathrm{cm}$ rolls without slipping down an inclined plane so that its centre moves with constant acceleration $w=2.50 \mathrm{cm} {\mathrm{s}}^{-2}\text{, }t=2.00 \mathrm{s}$ after the beginning of motion, its position corresponds to that shown in the figure. Find, 
$\left(a\right)$ the velocities of the points $A\text{,} B$ and $O$, 
$\left(b\right)$ the accelerations of these points.

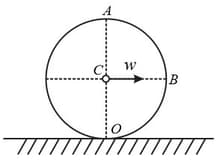
A cylinder rolls without slipping over a horizontal plane. The radius of the cylinder is equal to $r$. Find the curvature radii of trajectories traced out by the points $A$ and $B$.

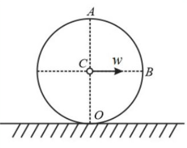
A solid body rotates with a constant angular velocity ${\omega }_0=0.50 \mathrm{rad} {\mathrm{s}}^{-1}$ about a horizontal axis $AB$. At the moment $t=0$ the axis $AB$ starts turning about the vertical with a constant angular acceleration ${\beta }_0=0.10 \mathrm{rad} {\mathrm{s}}^{-2}$. Find the angular velocity and angular acceleration of the body after $t=3.5 \mathrm{s}$.