Nishit K Sinha Solutions for Chapter: Measurement, Exercise 4: Benchmarking Test 4

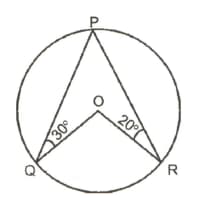
In the given figure, if $\angle \mathrm{OQP}=30°$ and $20°\text{, then }\angle \mathrm{QOR}$, then $\angle \mathrm{QOR}$ is equal to:

In the figure given below, $\mathrm{ABCD}$ is a square of side length $4\sqrt{2}$ units. Shaded parts are the sectors of the different circles with $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$, and $\mathrm{D}$as the centres. What is the area (in sq. units) of the shaded region?

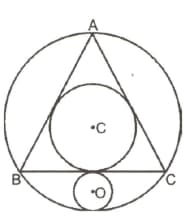
In the figure given below, $\mathrm{ABC}$ is an equilateral $\Delta$ of side length $3$units and circle with centre $\mathrm{C}$ is the in-circle. Another circle with centre $\mathrm{O}$ is drawn in such a way that side $\mathrm{BC}$ of the triangle $\mathrm{ABC}$ is tangent to the circle and circumcircle is having a point of tangency with this circle. What will be the length of the radius of the circle with centre $\mathrm{O}$ ?

In the figure given below, $∆\mathrm{ABC}$ is an equilateral triangle with side length $3$ units. Triangles are arranged inside this triangle in such a way that the circle with centre $\mathrm{G}$ is the incircle of the triangle $\mathrm{ABC}$ and the circle with centre $\mathrm{H}$ is formed on the circle with centre $\mathrm{G}$and so on. The next circle will be created on this circle with centre $\mathrm{H}$ and so on, and the infinite circles are created one above the other.

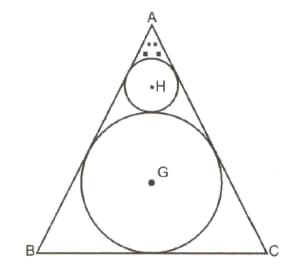
What is the sum of the radius of all such circles formed?

An octagon is inscribed in a circle. One set of alternate vertices forms a square of area $5$ units. The other set forms a rectangle area of $4$ units. What is the maximum possible area for the octagon (in sq. units)?

What is the largest number of the quadrilaterals formed by four adjacent vertices of an convex polygon of n sides that can have an inscribed circle?

There are two circles with centres at $\mathrm{A}$ and $\mathrm{B}$, respectively. The circle with centre A has a radius of $8$units and the circle with centre $\mathrm{B}$ has a radius of $6$units and the distance of $\mathrm{AB}$ is $12$units. Both the circles meet at points $\mathrm{P}$ and $\mathrm{S}$. A line through $\mathrm{P}$ meets the circles again at $\mathrm{Q}$ and $\mathrm{R}$ (with $\mathrm{Q}$ on the larger circle) in such a way that $\mathrm{Q} \mathrm{P}=\mathrm{P} \mathrm{R}$. Find the length of $\mathrm{Q} \mathrm{P}$.

A circle of $4$ units is taken. Now, $\mathrm{n}$ circles of the same radii are inserted in this circle $(1\le \mathrm{n}\le 10$, where $\mathrm{n}$ is a natural number) in such a way that they are encompassing the maximum possible areas of the circle and are inside the bigger circle along its circumference. (Obviously, for $\mathrm{n}=1$, radius of the inside circle will be same as the radius of the outside circle. Similarly, for $\mathrm{n}=2$, radius of the inside circle will be half of the outside bigger circle and so on.) For how many values of $\mathrm{n}$, radius of the circle will be an integer?