R S Aggarwal and Veena Aggarwal Solutions for Exercise 1: EXERCISE 12A

A chord of length $16 \mathrm{cm}$ is drawn in a circle of radius $10 \mathrm{cm}$. Find the distance of the chord from the center of the circle in centimetre.

In the given figure, the diameter $\mathrm{CD}$ of a circle with centre $\mathrm{O}$ is perpendicular to chord $\mathrm{AB}$ If $\mathrm{AB}=12 \mathrm{cm}\text{ and }\mathrm{CE}=3 \mathrm{cm}$  calculate the radius of the circle.

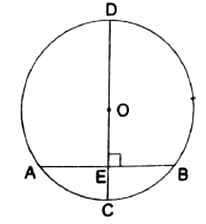
In the given figure, a circle with centre $\mathrm{O}$ is given in which a diameter $\mathrm{AB}$ bisects the chord $\mathrm{CD}$ at a point $\mathrm{E}$, such that $\mathrm{CE}=\mathrm{ED}=8 \mathrm{cm}$ and $\mathrm{EB}=4 \mathrm{cm}$. If the radius of the circle is $k \mathrm{cm}$, find the value of $k$

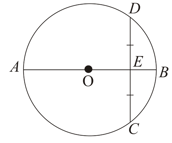
Two circles of radii $10 \mathrm{cm} \text{and} 8 \mathrm{cm}$ intersect each other, and the length of the common chord is $12 \mathrm{cm}$. If the distance between their centres is of the form $a+b\sqrt{c}$, then find the value of $a+b+c$.

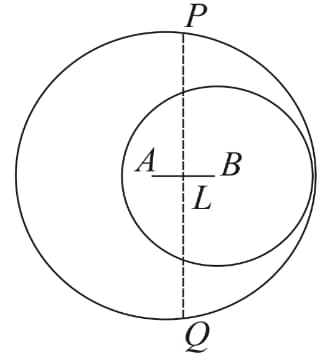
In the adjoining figure, two circles with centers at $\mathrm{A}$ and $\mathrm{B}$ and of radii $5 \mathrm{cm} \mathrm{and} 3 \mathrm{cm}$ touch each other internally. If the perpendicular bisector of $AB$ meets the bigger circle in$\mathrm{P} \mathrm{and} \mathrm{Q}$ then the length of $\mathrm{PQ}$ is $A\sqrt{6}$. Find the value of $A$.

$AB$ and $AC$ are two chords of a circle of radius $r$ such that $AB=2AC$. If $p$ and $q$ are the distances of $AB$ and $AC$ from the centre then prove that $4q^2=p^2+3r^2$.

An equilateral triangle of side $9 \mathrm{cm}$ is inscribed in a circle. If the radius of the circle is $k\sqrt{k} \mathrm{cm}$, then write the value of $k$.

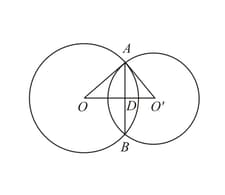
Two circles with centers  $O$ and $O\text{'}$ intersect at two points $A$ and $B. A$ line $PQ$ is drawn parallel to $OO\text{'}$ through $A$ or $B,$ intersecting the circles at $P$ and $Q$. Prove that $PQ = 2OO\text{'}$.