R S Aggarwal and Veena Aggarwal Solutions for Exercise 1: Exercise 7A
R S Aggarwal Mathematics Solutions for Exercise - R S Aggarwal and Veena Aggarwal Solutions for Exercise 1: Exercise 7A
Attempt the free practice questions from Exercise 1: Exercise 7A with hints and solutions to strengthen your understanding. Secondary School Mathematics for Class 10 solutions are prepared by Experienced Embibe Experts.
Questions from R S Aggarwal and Veena Aggarwal Solutions for Exercise 1: Exercise 7A with Hints & Solutions
In a is the bisector of .
If and , find and .
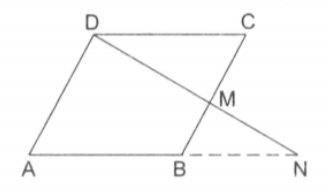
is a point on the side of a parallelogram . when produced meets produced at Prove that
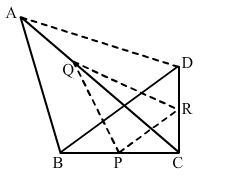
In , and are points on the sides and respectively such that . If then show that .
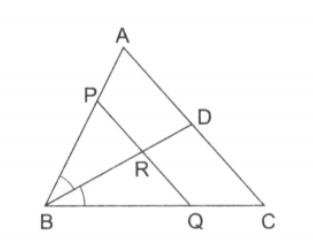
and lie on the same side of as shown in the figure. From a point on and are drawn, meeting at and at respectively. Prove that
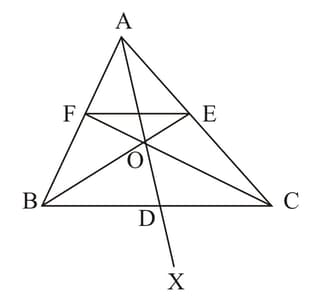
In the given figure, side of is bisected at and is any point on and produced meet and at and respectively, and is produced to so that is the midpoint of Prove that and show that
is a parallelogram in which is the midpoint of and is a point on such that . If produced meets at , prove that is the midpoint of .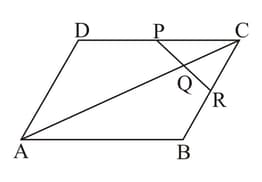
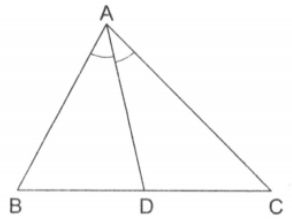
In the adjoining figure, is a triangle in which . If and are points on and respectively such that , show that the points and are concyclic.
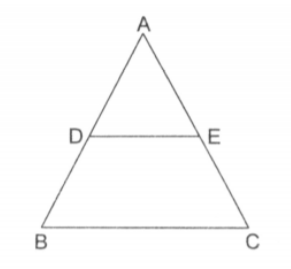
In , the bisector of meets at . A line meets and at , and respectively. Show that .