Kerala Board Solutions for Chapter: Circles, Exercise 1: Exercise 1

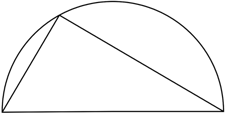
Suppose we draw a circle with the bottom side of the triangles in the picture as diameter. Find out whether the top corner of each triangle is inside the circle, on the circle or outside the circle.

For each diagonal of the quadrilateral shown, check whether the other two corners are inside, on or outside the circle with that diagonal as diameter.

If circles are drawn with each side of a triangle of sides $5$ centimetres, $12$ centimetres and $13$ centimetres, as diameters, then with respect to each circle, where would be the third vertex?

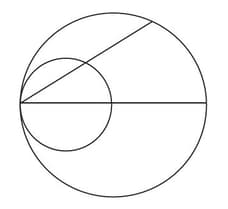
In the picture, a circle is drawn with a line as diameter and a smaller circle with half the line as diameter. Prove that any chord of the longer circle through the point where the circles meet is bisected by the small circle.

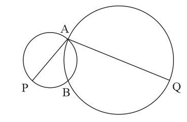
The two circles in the picture cross each other at $A$ and $B$. The points $P$ and $Q$ are the other ends of the diameters through $A$. Prove that $\mathrm{PQ}$ is parallel to the line joining the centres of the circles and is twice as long as this line.

Prove that the two circles drawn on the two equal sides of an isosceles triangle as diameters pass through the midpoint of the third side.

Prove that all four circles drawn with the sides of a rhombus as diameters pass through a common point.

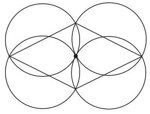
Prove that this is true for any quadrilateral with adjacent sides equal, as in the picture.

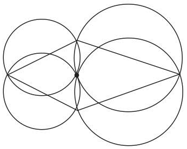
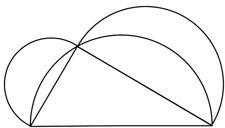
A triangle is drawn by joining a point on a semicircle to the ends of the diameter. Then semicircles are drawn with the other two sides as diameter. Prove that the sum of the areas of the blue and red crescents in the second picture is equal to the area of the triangle.