Kerala Board Solutions for Chapter: Similar Triangles, Exercise 1: Exercise 1

At two ends of a horizontal line, angles of equal size are drawn and two points on the slanted lines are joined. Explain how a line of length$6 \mathrm{cm}$ can be divided in the ratio $3 : 4$.

The midpoint of the bottom side of a square is joined to the ends of the top side and extended by the same length. The ends of these lines are joined and perpendiculars are drawn from these points to the bottom side of the square extended. Prove that the quadrilateral obtained thus is also a square.

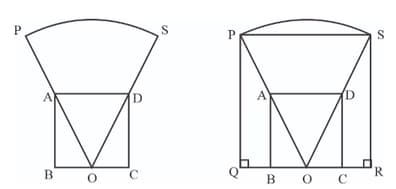
Explain how we can draw a square with two corners on a semicircle and the other two corners on its diameter as given in the figure.

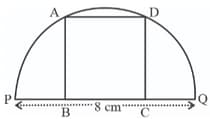
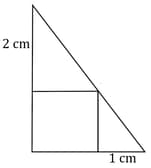
The picture shows a square drawn sharing one corner with a right triangle and the other three corners on the sides of this triangle. Calculate the length of a side of the square.

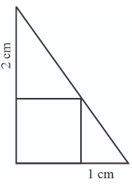
The picture shows a square drawn sharing one corner with a right triangle and the other three corners on the sides of this triangle.

What is the length of a side of the square drawn like this within a triangle of sides $3 \mathrm{cm}, 4 \mathrm{cm}$ and $5 \mathrm{cm}$.

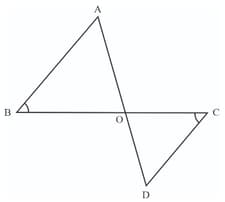
Two poles of heights $3 \mathrm{m}$ and $2 \mathrm{m}$ are erected upright on the ground and ropes are stretched from the top of each to the foot of the other.

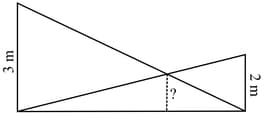
At what height  above the ground do the ropes cross each other?

Two poles of heights $3 \mathrm{m}$ and $2 \mathrm{m}$ are erected upright on the ground and ropes are stretched from the top of each to the foot of the other.

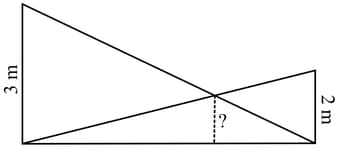
Taking the height of the poles as $a$ and $b$ and height above the ground of the point where the ropes cross each other as $h$, find the relation between $a, b$ and $h$.

Two poles of heights $3 \mathrm{m}$ and $2 \mathrm{m}$ are erected upright on the ground and ropes are stretched from the top of each to the foot of the other.

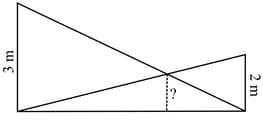
Prove that this height would be the same, whatever be the distance between the poles.