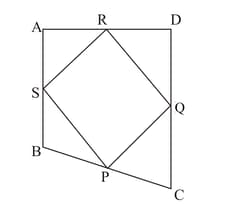
If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral. [Hint: Join and draw perpendicular from on .]


Important Questions on Areas of Parallelograms and Triangles
A point is taken on the side of a parallelogram . and are produced to meet at . Prove that
The diagonals of a parallelogram intersect at a point Through , a line is drawn to intersect at and BC at . Show that divides the parallelogram into two parts of equal area.
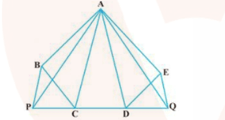
In given figure, and . Prove that
is a trapezium in which and . If and are respectively the mid-points of and , prove that: .
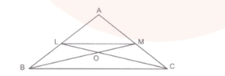
In , if and are the points on and , respectively such that Prove that .
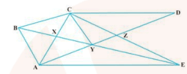
In the given figure, is any pentagon. drawn parallel to meets produced at and drawn parallel to meets produced at Prove that