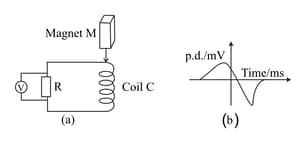
A bar magnet $M$ is dropped so that it falls vertically through the coil $C$. The graph obtained for voltage produced across the coil vs time is shown in Fig. 6.83 (b).

Explain the shape of the graph.

 

A bar magnet $M$ is dropped so that it falls vertically through the coil $C$. The graph obtained for voltage produced across the coil vs time is shown in Fig. 6.83 (b).

Why is the negative peak longer than the positive peak?

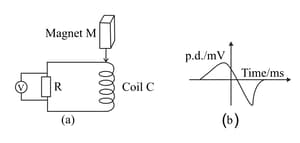
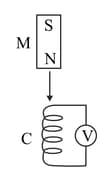
Figure 6.85 shows a bar magnet $M$ falling under gravity through an air-cored coil $C$. Plot a graph showing variation of induced emf ($\epsilon$) with time ($t$). What does the area enclosed by the $\epsilon -t$ curve depict?

A small square loop of wire of side $I$ is placed inside a large square loop of wire of side $L(L>>I)$. The loops are coplanar and their centres coincide [Fig. 6.86]. Find the mutual inductance of the system.

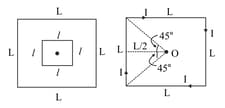
In Fig. 6.87, a rod closing the circuit moves along a U-shaped wire at a constant speed v under the action of the force $F$. The circuit is in a uniform magnetic field perpendicular to its plane. Calculate $F$ if the rate of generation of heat is $P$.

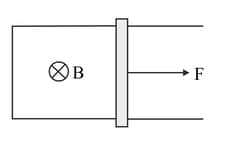
Figure 6.88 shows a long, rectangular, conducting loop of width $I$, mass $m$ and resistance $R$ placed partly in a perpendicular magnetic field $B$. With what velocity should it be pushed downwards so that it may continue to fall without any acceleration?

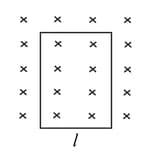
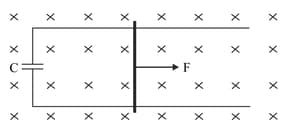
Figure 6.89 shows a wire of mass m and length $l$ which can slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field $B$. The rails are connected by a capacitor of capacitance $C$. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.

A rectangular wire frame, as shown in Fig. 6.90(a) is placed in uniform magnetic field directed upward and normal to the plane of the paper. The part $AB$ is connected to a spring. The spring is stretched and released when the wire $AB$ has come to the position $A\text{'} B\text{'} (t=0)$. Explain qualitatively how induced emf in the coil would vary with time. Neglect damping of oscillations of the spring.

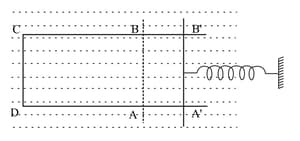
Figure 6.91 shows two long coaxial solenoids, each of length '$l$'. The outer solenoid has an area of cross-section $A_1$ and number of turns/length $n_1$. The corresponding values for the inner solenoid are $A_2$ and $n_2$. Write the expression for self inductance $L_1$, $L_2$ of the two coils and their mutual inductance $M$. Hence show that $M<\sqrt{L_1{L}_2}$.