HARD
JEE Advanced
IMPORTANT
Earn 100
A block with mass is connected by a massless spring with stiffness constant to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude about an equilibrium position . Consider two cases : (i) when the block is at and (ii) when the block is at . In both the cases, a particle with mass is softly placed on the block after which they stick to each other. Which of the following statement(s) is(are) true about the motion after the mass is placed on the mass ?
(a)The amplitude of oscillation in the first case changes by a factor of whereas in the second case it remains unchanged
(b)The final time period of oscillation in both the cases is same
(c)The total energy decreases in both the cases
(d)The instantaneous speed at of the combined masses decreases in both the cases.
16.67% studentsanswered this correctly

Important Questions on Oscillations
HARD
JEE Advanced
IMPORTANT
A particle of mass is attached to one end of a massless spring of force constant , lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time with an initial velocity . When the speed of the particle is , it collides elastically with a rigid wall. After this collision :
HARD
JEE Advanced
IMPORTANT
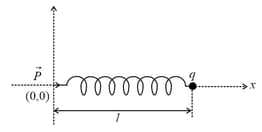
One end of a spring of negligible unstretched length and spring constant is fixed at the origin . A point particle of mass carrying a positive charge is attached at its other end. The entire system is kept on a smooth horizontal surface. When a point dipole pointing towards the charge is fixed at the origin, the spring gets stretched to a length and attains a new equilibrium position (see figure below). If the point mass is now displaced slightly by from its equilibrium position and released, it is found to oscillate at frequency The value of is _______.
HARD
JEE Advanced
IMPORTANT
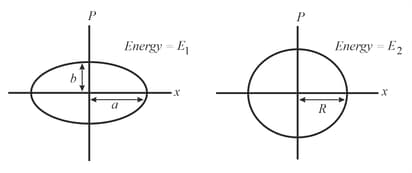
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies and and have total energies and , respectively. The variations of their momenta with positions are shown in the figures. If and , then the correct equation(s) is (are)