A charged, conducting sphere of radius $5.5 \mathrm{cm}$ sets up a potential of $75 \mathrm{V}$ at a radial distance of $2.2 \mathrm{m}$ (with $V=0$ set at infinity).

(a) What is the potential on the sphere's surface?
(b) What is the surface charge density?

The figure shows a thin plastic rod of length $L=12.0 \mathrm{cm}$ and uniform positive charge $Q=47.9 \mathrm{fC}$ lying on the $x$-axis. With $V=0$ at infinity, find the electric potential at a point $P_1$ on the axis, at a distance $d=2.50 \mathrm{cm}$ from the rod.

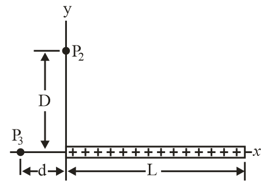
The figure shows a thin plastic rod of length $L=13.5 \mathrm{cm}$ and uniform charge $43.6 \mathrm{fC}$ .

(a) In terms of distance $d$, find an expression for the electric potential at a point $P_1$.

(b) Next, substitute variable $x$ for $d$ and find an expression for the magnitude of the component $E_{\mathrm{x}}$ of the electric field at $P_1.$

(c) What is the direction of $E_{\mathrm{x}}$ relative to the positive direction of the $x$-axis? 

(d) What is the value of $E_{\mathrm{x}}$ at $P_1$ for $x=d=6.60 \mathrm{cm}?$

(e) From the symmetry in figure determine $E_{\mathrm{y}}$ at $P_1$.

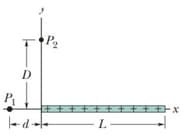
(a) Figure $\left(a\right)$ shows a nonconducting rod of length $L=6.00 \mathrm{cm}$ and uniform linear charge density $\lambda =+7.07 \mathrm{pC} {\mathrm{m}}^{-1}$. Assume that the electric potential is defined to be $V$$=0$ at infinity. What is $V$ at point $P$ at a distance $d=8.00 \mathrm{cm}$ along the rod's perpendicular bisector?

(b) Figure $\left(b\right)$ shows an identical rod except that one half is now negatively charged. Both halves have a linear charge density of magnitude $3.68 \mathrm{pC} {\mathrm{m}}^{-1}$. With $V=0$ at infinity, what is $V$ at $P?$ Is the potential at $P$ positive, negative or zero if $P$ is moved in the plane of the figure by a distance of $\frac{L}{4}$ (c) upward and (d) leftward?

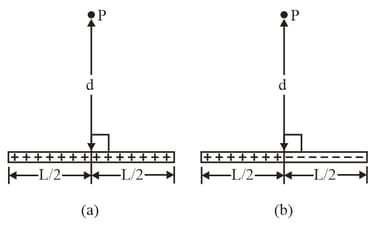
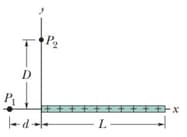
The thin plastic rod of length $L=12.0 \mathrm{cm}$ as shown in figure, has a non-uniform linear charge density $\text{λ}=cx \mathrm{C} {\mathrm{m}}^{-1},$ where, $c=49.9 \mathrm{pC} {\mathrm{m}}^{-2}$ (a) With $V=0$ at infinity, find the electric potential at point $P_2$ on the $y$-axis at $y=D=3.56 \mathrm{cm}.$ (b) Find the electric field component $E_{\mathrm{y}}$ at $P_2$ (c) Why cannot the field component $E_{\mathrm{x}}$ at $P_2$ be found using the result of (a)?

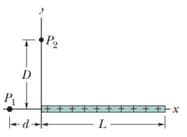
In the figure, particles with the charges $q_1=+15e$ and $q_2=-5e$ are fixed with a separation of $d=24.0 \mathrm{cm}.$ With electric potential defined to be $V=0$ at infinity, what are the finite (a) positive and (b) negative values of $x$ at which the net electric potential on the $x$-axis is zero?

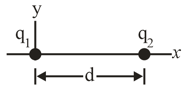
Two particles of charges $q_1$ and $q_2$ are separated by a distance $d$ in the figure. The net electric field due to the particles is zero at $x=d/4.$

(a) With$V=0$ at infinity, locate (in terms of $\mathrm{d}$) any point on the $\mathrm{x}$-axis (other than at infinity) at which the electric potential due to the two particles is zero.

(b) If, instead the net electric potential is $0$ at $x=d/4,$ find (in terms of $d$) the coordinates of any point (other than at infinity) at which the net electric field is zero.

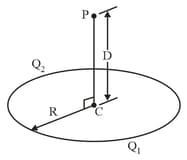
Plastic rod has been bent into a circle of radius $R=8.20 \mathrm{cm}$ It has a charge $Q_1=+7.07 \mathrm{pC}$ uniformly distributed along one quarter of its circumference and a charge $Q_2=-6 Q_1$ is uniformly distributed along the rest of the circumference (as shown in fig.)  With $V=0$ at infinity, what is the electric potential at (a) the center $C$ of the circle and (b) point $P$ on the central axis of the circle at distance $D=2.05 \mathrm{cm}$ from the center?