A cord with negligible mass is wrapped around a pulley that is a uniform disk of mass and radius and that can rotate without friction about its central axis. A bucket is attached at the free end of the cord hanging down from the pulley and then released at time The cord begins to unwrap from the pulley as the bucket descends. At , through how many rotations has the pulley turned (the bucket is still descending)?

Important Questions on Rotation
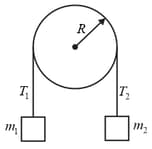
In the figure shown below, block has mass , block has mass , and the pulley, which is mounted on a horizontal axle with negligible friction, has radius . When released from rest, block falls in without the cord slipping on the pulley.
What is the magnitude of the acceleration of the blocks? What are
tension and
tension ?
What is the magnitude of the pulley's angular acceleration?
What is its rotational inertia?
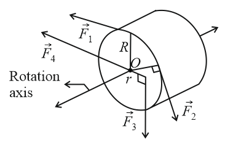
In the figure shown below a cylinder having a mass of can rotate about its central axis through point . Forces are applied as shown: . Also, , and . Find the
magnitude and
direction of the angular acceleration of the cylinder. (During the rotation, the forces maintain their same angles relative to the cylinder.)
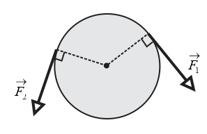
In the figure shown below, a uniform disk that can rotate around its centre like a merry-go-round. The disk has a radius of and a mass of gram and is initially at rest. Starting at time , two forces are to be applied tangentially to the rim as indicated so that at time , the disk has an angular velocity of counter-clockwise. Force has a magnitude of . What is magnitude of ?
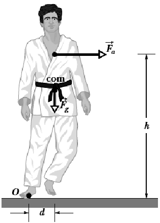
In a judo foot-sweep move, you sweep your opponent's left foot out from under him while pulling on his gi (uniform) toward that side. As a result, your opponent rotates around his right foot and onto the mat. In the figure shown below, a simplified diagram of your opponent as you face him with his left foot swept out. The rotational axis is through point . The gravitational force on him effectively acts at his center of mass, which is a horizontal distance from point . His mass is and his rotational inertia about point is . What is the magnitude of his initial angular acceleration about point if your pull on his gi is (a) negligible and (b) horizontal with a magnitude of and applied at height ?
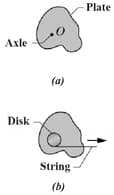
In the figure shown below, an irregularly shaped plastic plate with uniform thickness and density (mass per unit volume) is to be rotated around an axle that is perpendicular to the plate face and through point . The rotational inertia of the plate about that axle is measured with the following method. A circular disk of mass , and radius is glued to the plate, with its center aligned with point (figure ). A string is wrapped around the edge of the disk the way a string is wrapped around a top. Then the string is pulled for . As a result, the disk and plate are rotated by a constant force of that is applied by the string tangentially to the edge of the disk. The resulting angular speed is . What is the rotational inertia of the plate about the axle?
In the figure shown below particles and , each of mass , fixed to the ends of a rigid massless rod of length , with , and . The rod is held horizontally on the fulcrum and then released. What are the magnitudes of the initial accelerations of
particle and
particle ?
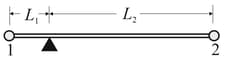
A pulley, with a rotational inertia of about its axle and a radius of , is acted on by a force applied tangentially at its rim. The force magnitude varies in time as , with in newton and in second. The pulley is initially at rest. At , what are its
(a) angular acceleration and
(b) angular speed?
