Two non-viscous, incompressible and immiscible liquids of densities ρ and 1 . 5 ρ are poured into the two limbs of a circular tube of radius R and small cross-section kept fixed in a vertical plane as shown in figure. Each liquid occupies one-fourth the circumference of the tube. (i) Find the angle θ that the radius to the interface make with the vertical in equilibrium position. (ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations.

(i) Let the liquid of density 1.5 ρ occupy the left portion A B and the liquid of density ρ occupy the right portion B C of the tube. The pressure at the lowest point D due to the liquid on the left is P 1 = R − R sin θ 1.5 ρ The pressure due to the liquid on the right is P 2 = R sin θ + R cos θ ρ g + R − R cos θ 1.5 ρ g Since the liquid are in equilibrium P 1 = P 2 or R − R sin θ 1.5 ρ g = R sin θ + R cos θ p g + R − R cos θ 1.5 ρ g Solving, we get tan θ = 0.2 or θ = tan − 1 0.2 (ii) Let the whole liquid be given a small angular displacement α towards. Then the pressure difference between the right and the left limbs is d P = P 2 − P 1 = R sin θ + α + R cos θ + α ρ g + [ R − R cos θ + α 1.5 ρ g − [ R − R sin θ + α 1.5 ρ g = R ρ g 2.5 sin θ + α − 0.5 cos θ + α = R ρ g 2.5 sin θ cos α + cos θ sin α − 0.5 cos θ cos α − sin θ sin α For small α sin α ≈ α , cos α ≈ 1 ∴ d P = R ρ g 2.5 sin θ + 2.5 α cos θ − 0.5 cos θ + 0.5 α sin θ As tan θ = 0.2 , sin θ 0.2 1.04 ≈ 0.2 , cos θ = 1 1.04 ≈ 1 ∴ d P = R ρ g 2.5 × 0.2 + 2.5 α − 0.5 + 0.5 × 0.2 α = R ρ g 2.6 α = 2.6 ρ g where y = R α , the linear displacement. ∴ Restoring force F = 2.6 ρ g A y This shows that F ∝ y Hence the motion is simple harmonic with force constant k = 2.6 ρ g A Now, total mass of the liquid m = 2 π R 4 A ρ + 2 π R 4 A 1.5 p = 5 π R Α ρ 4 ∴ Time period T = 2 π m k = 2 π ρ 5 π Α ρ 4 × 2.6 ρ g A = π ρ 1.93 π R 9.8 = 2.47 R seconds,

In the figure shown, the spring are connected to the rod at one end and at the midpoint. The rod is hinged at its lower end. (i) Find the minimum value of k for rotational SHM of the rod (Mass m , length L ) (ii) If k = mg L − 1 then find the angular frequency of oscillations of the rod.

(i) The rod performs SHM if the angular displacement of the rod is small (assumed) Restoring torque > Disturbing torque also for a small angular displacement we have θ = x 1 l / 2 , x 1 = θ l 2 , f 1 = K θ l 2 θ = x 2 l , x 2 = θ l , f 2 = K θ l τ = L 2 × F 1 × L × F 2 ≥ m g sin θ L 2 ⇒ L 2 K θ L 2 + L K θ L ≥ m g θ L 2 ⇒ 5 4 K θ L 2 ≥ m g θ L 2 ⇒ K ≥ 2 m g 5 L (ii) If the rod is displacement through an angle θ , then − k L θ L − k L 2 θ L 2 + M g L 2 θ = M L 2 3 α k = M g L ⇒ − 9 k θ 4 M = α ⇒ ω = 3 2 k m

HARD

JEE Main/Advance

IMPORTANT

Earn 100

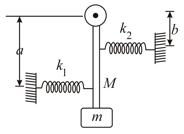
A mass $M$ is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass $m$ dropped from certain height sticks to the mass $M$ after colliding with it. The oscillations they perform reach to height ' $a$ ' above th original level of scales & depth ' $b$ ' below it.

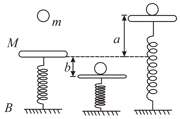
(i) find the constant of force of the spring

(ii) find the oscillation frequency.

(iii) what is the height above the initial level from which the mass $m$ was dropped?

Important Questions on Simple Harmonic Motion

HARD

JEE Main/Advance

IMPORTANT

Beta Question Bank for Engineering: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-4>Q 10

Two non-viscous, incompressible and immiscible liquids of densities

ρ

and

1.5 ρ

are poured into the two limbs of a circular tube of radius

R

and small cross-section kept fixed in a vertical plane as shown in figure. Each liquid occupies one-fourth the circumference of the tube.

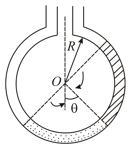
Question Image

(i) Find the angle $θ$ that the radius to the interface make with the vertical in equilibrium position.

(ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations.

HARD

JEE Main/Advance

IMPORTANT

Beta Question Bank for Engineering: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-4>Q 12

One rope of a swing is fixed above the other rope by

b

. The distance between the poles of the swing is

a

. The lengths

l_{1}

and

l_{2}

of the ropes are such that

l_{1}^{2} + l_{2}^{2} = a^{2} + b^{2}

. (Fig.) Determine the period

T

of small oscillations of the swing, neglecting the height of the swining person in comparison with the above lengths.

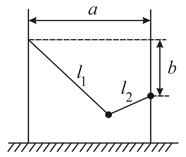
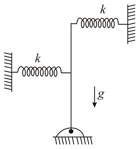
Question Image

HARD

JEE Main/Advance

IMPORTANT

Beta Question Bank for Engineering: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-4>Q 13

A massless road rigidly fixed at

O

. A string carrying a mass

m

at one end is attached to point

A

on the rod so that

O A = a

. At another point

B (O B = b)

pf the rod, a horizontal spring of force constant

k

is attached as shown. Find the period of small vertical oscillations of mass

m

around its equilibrium position

Question Image

MEDIUM

JEE Main/Advance

IMPORTANT

Beta Question Bank for Engineering: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-4>Q 14

A life operator hung an exact pendulum clock on the lift wall in a lift in a building to know end of the working day. The lift moves with an upward & downward accelerations during the same time (according to a stationary clock), the magnitudes of the acceleration remaining unchanged. Will the operator work for more or less than required time.

MEDIUM

JEE Main/Advance

IMPORTANT

Beta Question Bank for Engineering: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-4>Q 15

In the figure shown, the spring are connected to the rod at one end and at the midpoint. The rod is hinged at its lower end.

Question Image

(i) Find the minimum value of $k$ for rotational $SHM$ of the rod (Mass $m$ , length $L$ )

(ii) If $k = mg L^{- 1}$ then find the angular frequency of oscillations of the rod.

HARD

JEE Main/Advance

IMPORTANT

Beta Question Bank for Engineering: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-4>Q 16

Two identical balls

A

and

B

each of mass

0.1 kg

are attached to two identical massless springs. The spring mass system is constrained to move inside a rigid smooth pipe in the form of a circle as in fig. The pipe is fixed in a horizontal plane. The centres of the ball can move in a circle of radius

0.06 m

. Each spring has a natural length

0.06 πm

and force constant

0 .1 N m^{- 1}

. Initially both the balls are displaced by an angle of

θ = π / 6

radian with respect to diameter

P Q

of the circle and released from rest

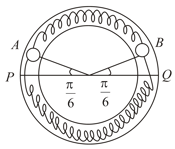
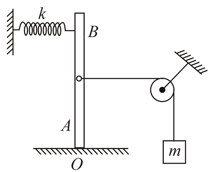
Question Image

(i) calculate the frequency of oscillation of the ball $B$ .

(ii) what is the total energy of the system

(iii) find the speed of the ball $A$ when $A$ and $B$ are at the two ends of the diameter $P Q$ .

HARD

JEE Main/Advance

IMPORTANT

Beta Question Bank for Engineering: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-4>Q 17

A rod of mass

M

and length

L

is hinged at its one end and carries a block of mass

m

at its other end.

A

spring of force constant

k_{1}

is installed at distance a from the hinge and another of force constant

k_{2}

at a distance

b

as shown in the figure. If the whole arrangement rests on a smooth horizontal table top. find the frequency of vibration.

Question Image

HARD

JEE Main/Advance

IMPORTANT

Beta Question Bank for Engineering: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-4>Q 18

The following equation represent transverse wave;

$z_{1} = A \cos (k x - ω t), z_{2} = A \cos (k x + ω t), z_{3} = A \cos (k y - ω t)$

Identify the combination (s) of the waves which will produce. (i) standing wave (s) (ii) a wave travelling in the direction making an angle of $45 °$ with the positive $x$ and positive $y$ -axis. In each case, find the position at which the resultant intensity is always zero.

Important Questions on Simple Harmonic Motion

Learn and Prepare for any exam you want !