A massive but uniform rope of length $L$ is suspended from a ceiling.
(a) The velocity of a transverse wave traveling on the string as a function of the distance from the lower end is ${\left(gx\right)}^a$.

(b) If the rope is given a sudden sideways jerk at the bottom, the timeit will take for the pulse to reach the ceiling is $\sqrt{\frac{bL}{g}}$.

(c) A particle is dropped from the ceiling at that instant the bottom end is given the jerk, the pulse will meet the particle at $\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$c$}\right.$.

Then the value of $\left(a+b+c\right)$ is:

A $200 \mathrm{Hz}$ wave with amplitude $1 \mathrm{mm}$ travels on a long string of linear mass density $6 \mathrm{g} {\mathrm{m}}^{-1}$ kept under a tension of $60 \mathrm{N}$.

(a) Find the average power transmitted across a given point on the string.

(b) Find the total energy associated with the wave in a $2.0 \mathrm{m}$ long portion of the string.

A tuning fork of frequency $440 \mathrm{Hz}$ is attached to a long string of linear mass density $0.01 \mathrm{kg} {\mathrm{m}}^{-1}$ kept under a tension of $49 \mathrm{N}$. The fork produces transverse waves of amplitude $0.50 \mathrm{mm}$ on the string.

(a) The wave speed is $x$.

(b) The maximum speed of the string is $y$.

(c) The average rate is the tuning fork transmitting energy to the string is $z$.

The value of the $\frac{xy}{z}$$\cong 1n6$. Then find the value of $n$.

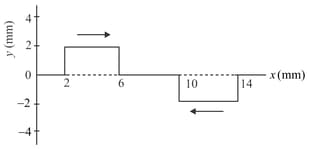
Figure shows two wave pulses at $t=0$ travelling on a string in opposite directions with the same wave speed $50 \mathrm{cm} {\mathrm{s}}^{-1}$. Point the values on graph for the string at $\mathrm{t}=4 \mathrm{ms}, 6 \mathrm{ms}, 8 \mathrm{ms},$ and $12 \mathrm{ms}$.

Two waves, each having a frequency of $100 \mathrm{Hz}$ and a wavelength of $2·0 \mathrm{cm},$ are travelling in the same direction on a string.  the 

(a) at the same place, if the second wave was produced $0·015 \mathrm{s}$  after the first one then phase difference between the waves is $\alpha \pi \mathrm{rad}$ .

(b) If the two waves were produced at the same instant but the first one was produced with a distance $4·0 \mathrm{cm}$ behind the second one then phase difference between the waves is $\beta \pi \mathrm{rad}$ .

(c) If each of the waves has an amplitude of $2·0 \mathrm{mm},$ then the amplitudes of the resultant waves in part (a) and (b) are $\gamma \mathrm{mm} \mathrm{and} \mathrm{\sigma } \mathrm{mm}$.

Find $\alpha +\beta +\gamma +\sigma$.