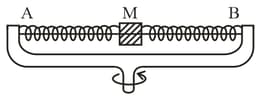
A non-deformed spring, whose ends are fixed, has a stiffness $k=13 \mathrm{N} {\mathrm{m}}^{-1}$. A small body of mass $m=25 \mathrm{g}$ is attached at the point removed from one of the ends by, $\mathrm{\eta }=\frac{1}{3}$ of the spring's length. Neglecting the mass of the spring, find the period of small longitudinal oscillations of the body. The force of gravity is assumed to be absent.

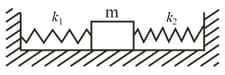
Determine the period of small longitudinal oscillations of a body with mass $m$ in the system shown in the figure. The stiffness values of the springs are $x_1$ and $x_2$. The friction and the masses of the springs are negligible.

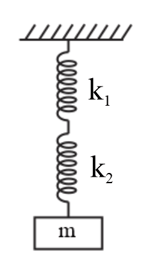
Find the period of small vertical oscillations of a body with mass $m$ in the system illustrated in the figure. The stiffness values of the springs are $k_1$ and $k_2$, their masses are negligible.

A small body of mass $m$ is fixed to the middle of a stretched string of length $2l$. In the equilibrium position the string tension is equal to $T_0$. Find the angular frequency of small oscillations of the body in the transverse direction. The mass of the string is negligible, the gravitational field is absent. Assume $\sin \theta =\theta$ for smaller values of $\theta .$

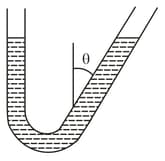
Determine the period of oscillations of mercury of mass $\mathrm{m}=200 \mathrm{g}$ poured into a bent tube whose right arm forms an angle $\mathrm{\theta }=30°$ with the vertical. The cross-sectional area of the tube is, $S=0.50 {\mathrm{cm}}^2$. The viscosity of mercury is to be neglected. Take $g=9.8 \mathrm{m} {{\mathrm{s}}^{-}}^2$.

A uniform rod is placed on two spinning wheels as shown in figure. The axes of the wheels are separated by a distance $l=20 \mathrm{cm}$, the coefficient of friction between the rod and the wheels is, $k=0.18$. Demonstrate that in this case the rod performs harmonic oscillations. Find the period of these oscillations. Take $g=9.8 \mathrm{m} {{\mathrm{s}}^{-}}^2$

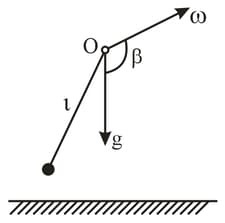
Find the period of small oscillations of a mathematical pendulum of length $l$ if its point of suspension $O$ moves relative to the Earth's surface in an arbitrary direction with a constant acceleration $w$ as shown in the figure. Calculate that period if $l=21 \mathrm{cm}, w=\frac{g}{2}$ and the angle between the vectors $w$ and $g$ equals $\mathrm{\beta }=120°$.

In the arrangement shown in the figure, the sleeve $M$ of mass $m=0.20 \mathrm{kg}$ is fixed between two identical springs whose combined stiffness is equal to $x=20 \mathrm{N} {\mathrm{m}}^{-1}$. The sleeve can slide without friction over a horizontal bar $AB$. The arrangement rotates with a constant angular velocity $\omega =4.4 \mathrm{rad} {\mathrm{s}}^{-1}$ about a vertical axis passing through the middle of the bar. Find the period of small oscillations of the sleeve. At what values of $\omega$ will there be no oscillations of the sleeve?