A small solid cone of radius $4 \mathrm{cm}$ and having a slant height $6 \mathrm{cm}$ is mounted on a bigger solid cone of radius $6 \mathrm{cm}$ and having a slant height $10 \mathrm{cm}$ with a common base. If the surface area of the combined figure is $k {\mathrm{cm}}^2$.

Then find the value of $k$.

Take $\left[\mathrm{\pi }=3.14\right]$

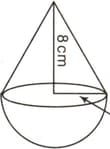
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is $6 \mathrm{cm}$ each and the slant height of the cone is $5 \mathrm{cm}$. 

 Find the volume of the solid.

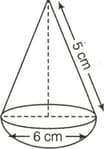
In the given figure, a hemisphere of radius $6 \mathrm{cm}$ surmounted by a right circular cone of base radius $6 \mathrm{cm}$ The height of the cone is $8 \mathrm{cm}$

If the total surface area of the solid is equal to $k c{m}^2$, then find the value of $k$. [Take $\mathrm{\pi }=3.14$]

In the given figure, a hemisphere of radius $6 \mathrm{cm}$ Surmounted by a right circular cone of base radius $6 \mathrm{cm}$. The height of the cone is $8 \mathrm{cm}$.

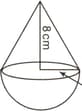
Calculate the volume of the solid. [Take$\mathrm{\pi }$  = 3.14]

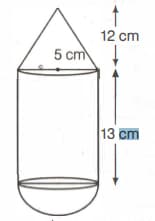
In the given figure, it shows a metal container in the form of a cylinder surmounted by a hemisphere of the same radius. The internal height of the cylinder is $7\mathrm{m}$ and the internal radius is $3.5\mathrm{m}$. Calculate the total area of the internal surface, excluding the base (in $m^2$ ).

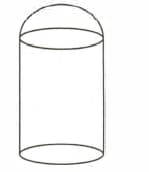
In the given figure, it shows a metal container in the form of a cylinder surmounted by a hemisphere of the same radius. The internal height of the cylinder is $7 \mathrm{m}$ and the internal radius is $3.5 \mathrm{m}$.

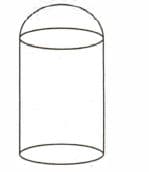
Calculate the internal volume of the container $\left(\mathrm{in} {\mathrm{m}}^3\right)$.

In the given figure, toy is in the shape of a right· circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are $13 \mathrm{cm}$ and $5 \mathrm{cm}$,respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is $12 \mathrm{cm}$