A solid rectangular block of metal $49 \mathrm{cm}\times 44 \mathrm{cm}\times 18 \mathrm{cm}$ is melted and formed into a solid sphere. Calculate the radius of the sphere

A certain number of metallic cones, each of radius $2 \mathrm{cm}$ and height $3 \mathrm{cm}$ are melted and recast into a solid sphere of radius $6 cm$. Find the number of cones.

The given block is made of two solids; a cone and a sphere. If the height and the base radius of the cone are $9\text{ cm,}$ $7 \mathrm{cm}$, respectively and the radius of the sphere is $5 \mathrm{cm}$, if the volume of the block is equal to $k c{m}^2$, then find the value of $k$.  Take $\left[\mathrm{\pi }=3.14\right]$

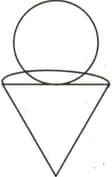
A small solid cone of radius $4 \mathrm{cm}$ and having a slant height $6 \mathrm{cm}$ is mounted on a bigger solid cone of radius $6 \mathrm{cm}$ and having a slant height $10 \mathrm{cm}$ with a common base. If the surface area of the combined figure is $k {\mathrm{cm}}^2$.

Then find the value of $k$.

Take $\left[\mathrm{\pi }=3.14\right]$

The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is $6 \mathrm{cm}$ each and the slant height of the cone is $5 \mathrm{cm}$. 

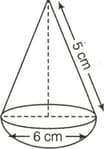
 Find the volume of the solid.