A solid sphere of radius $R$ has moment of inertia $I$ about its geometrical axis. If it is melted into a disc of radius $r$ and thickness $t$. If its moment of inertia about the tangential axis (which is perpendicular to plane of the disc) is also equal to $I$, then the value of $r$ is equal to:

Statement-I: Two cylinders, one hollow (metal) and the other solid (wood), with the same mass and identical dimensions, are simultaneously allowed to roll without slipping down an inclined plane from the same height. The hollow cylinder will reach the bottom of the inclined plane first.

and

Statement-2: By the principle of conservation of energy, the total kinetic energies of both the cylinders are identical when they reach the bottom of the incline.

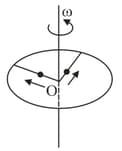
A ring of mass $M$ and radius $R$ is rotating with angular speed $\omega$ about a fixed vertical axis passing through its centre $O$ with two point masses each of mass $\frac{M}{8}$ at rest at $O$. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant, the angular speed of the system is $\frac{8}{9}\omega$ and one of the masses at a distance of $\frac{3}{5}R$ from $O$. At this instant, the distance of the other mass from $O$ is:

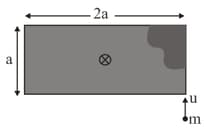
A uniform rectangular plate of mass $m$ which is free to rotate about the smooth vertical hinge passing through the centre and perpendicular to the plate is lying on a smooth horizontal surface. A particle of mass $m$ moving with speed $u$ collides with the plate and sticks to it as shown in the figure. The angular velocity of the plate after the collision will be:

A particle of mass $m$ is moving horizontally at speed $v$ perpendicular to a uniform rod of length $d$ and mass, $M=6m$. The rod is hinged at centre $O$ and can freely rotate in horizontal plane about a fixed vertical axis passing through its centre $O$. The hinge is frictionless. The particle strikes and sticks to the end of the rod. The angular speed of the system just after the collision is,

A circular disk of moment of inertia $I_t$ is rotating in a horizontal plane, about its symmetry axis, with a constant angular speed ${\omega }_i$. Another disk of moment of inertia $I_b$ is dropped coaxially onto the rotating disk. Initially the second disk has zero angular speed. Eventually both the disks rotate with a constant angular speed ${\omega }_f$.The energy lost by the initially rotating disk to friction is: