A string fixed at both ends has length $\mathrm{L}$ vibrates in its fundamental mode at a frequency $\nu$ and a maximum amplitude $A$.
(a) If the wavelength and the wave number are $\alpha L \mathrm{and} \frac{\mathrm{\beta \pi }}{\mathrm{L}}$.
(b) Taking origin at one end of the string and the $x-$axis along the string. Take the Y-axis along the direction of the displacement. Take $t=0$ at the instant when the middle point of the string passes through its mean position and is going towards the positive $y-$direction. If the equation describing the standing wave is $y=A\sin \left(\frac{\pi x}{L}\right)\sin \left(\gamma \pi \nu t\right)$.

Find $\alpha +\beta +\gamma$.

A $2$ m-long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is $200 \mathrm{m} {\mathrm{s}}^{-1}$ and the amplitude is $0.5 \mathrm{cm}$
(a) If the frequency and wavelength are$\alpha \mathrm{m} \& \mathrm{\beta } \mathrm{Hz}$ .
(b)  The equation giving the displacement of different points as a function of time is $(0.5 \mathrm{cm})\sin \left[\left(\pi {\mathrm{m}}^{-1}\right)\mathrm{x}\right]\cos \left[\left(\gamma \pi {\mathrm{s}}^{-1}\right)\mathrm{t}\right]$. Assume X-axis along the string with the origin at one end and $t=0$ at the instant when the point $x=50 \mathrm{cm}$ has reached its maximum displacement.

Find $\alpha +\beta +\gamma$.

The equation for vibrating a string, fixed at both ends vibrating in its third harmonic, is given by $y=\left(0.4 \mathrm{cm}\right)\sin \left[\left(0.314 {\mathrm{cm}}^{-1}\right)\mathrm{x}\right]\cos \left[\left(600 \pi {\mathrm{s}}^{-1}\right)t\right]$ What is the speed of two travelling waves that can interfere to give this vibration in $m{s}^{-1}$?

The equation for a standing wave, produced on a fixed string at both ends, is

$y=\left(0.4\mathrm{cm}\right)\sin \left[\left(0.314{\mathrm{cm}}^{-1}\right)x\right]\cos \left[\left(600{\mathrm{\pi s}}^{-1}\right)t\right]$

What could be the smallest length of the string?

The figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning fork. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. The density of the material of the block is given as $k\times {10}^3 kg m^{-3}$. Find the value of $k.$

A $2.00 \mathrm{m}$ long rope, having a mass of $80 \mathrm{g},$ is fixed at one end and is tied to a light string at the other end. The tension in the string is$256 \mathrm{N}$.

(a) Find the frequencies of the fundamental and the first two overtones.
(b) Find the wavelength in the fundamental and the first two overtones.

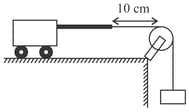
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is $120 \mathrm{Hz}$. If the movable support is pushed to the right by $10 \mathrm{cm}$ so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?