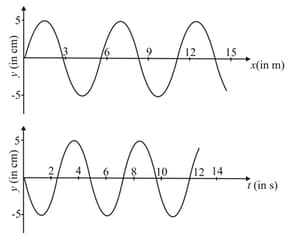
A transverse wave is travelling along a horizontal string. The first figure is the shape of the string at an instant of time. The second picture is a graph of the vertical displacement of a point on the string as a function of time. Find the wave speed.

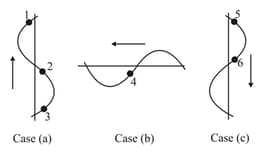
The figures of case (a), case (b) and case (c) shows the shape of three strings on which sinusoidal transverse waves are propagating. The arrows in the diagram indicate the direction of wave propagation. Out of the $6$ particles marked $(1,2,3, 4,5,6)$ which particles have their instantaneous velocity and acceleration both directed towards their mean position.

A wave pulse is travelling along $+x$ direction on a string at $2 \mathrm{m}/\mathrm{s}$. Displacement $y$(in $\mathrm{cm}$ ) of the particle at $x=0$ at any time $t$ is given by $2/\left(t^2+1\right)$. Find

$\left(a\right)$ Expression of the function $y=\left(x,t\right)$ i.e. displacement of a particle at position $x$ and time $t$.

$\left(b\right)$Draw the shape of the pulse at $t=0$ and $t=1 \mathrm{s}$.

A transverse pulse moving on a long string along $x$-axis is given as, $y=\frac{2}{(5x-3t{)}^2+1}$, where $x$ is measured in meter $y$ in centimeter and $t$ is measured in seconds. Find the

particle velocity as the function of $x$and $t$

A transverse pulse moving on a long string along $x$-axis is given as, $y=\frac{2}{(5x-3t{)}^2+1}$, where $x$ is measured in meter $y$ in centimeter and $t$ is measured in seconds. Find the

particle velocity at $x=\pm 1 \mathrm{m},t=0\sec$.

$A, B$ and $C$ are the three particles of a medium which are equally separated and lie along the $x$-axis. When a sinusoidal transverse wave of wavelength $\lambda$ propagates along the $x$-axis, the following observations are made:

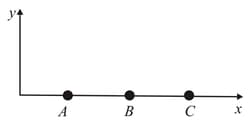
(i) A and B have the same speed.
(ii) A and C have the same velocity. Find

the minimum distance between A and B and