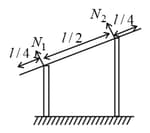
A uniform rod of length $l$ is placed symmetrically on two walls as shown in figure. The rod is in equilibrium. If $N_1$ and $N_2$ are the normal forces exerted by the walls on the rod, then,

STATEMENT 1: The total translational kinetic energy of all the molecules of a given mass of an ideal gas is $1.5$ times the product of its pressure and its volume. Because

STATEMENT 2: The molecules of gas collide with each other and the velocities of the molecules change due to the collision.

Assertion: If two different axes are at same distance from centre of mass of a rigid body, then moment of inertia of the given rigid body about both axes will always be same.

Reason: A thin uniform rod is undergoing fixed axis rotation about one of its ends with variable angular acceleration. Then, the acceleration vector of any two moving points on the rod cannot be parallel at an instant of time.

Assertion: A rigid disc rolls without slipping on a fixed rough horizontal surface with uniform angular velocity. Then, the acceleration of lowest point on the disc is zero.

Reason: For a rigid disc rolling without slipping on a fixed rough horizontal surface, the velocity of the lowest point on the disc may be non-zero.

Assertion : If the momentum of a particle is constant, then its angular momentum will also be constant

Reason : When net external force on an object is zero, then external torque on the object will also be zero.

Assertion: A thin uniform rod is undergoing fixed axis rotation about one of its ends with variable angular acceleration. The acceleration vector of any two moving points on the rod can not be parallel at any instant of time.

Reason: For a rod undergoing fixed axis rotation, the velocity of any two moving points on the rod at different distances from the centre of rotation is different.

Assertion: A rigid disc rolls without slipping on a fixed rough horizontal surface with uniform angular velocity. Then the acceleration of the lowest point on the disc is zero.

Reason: For a rigid disc rolling without slipping on a fixed rough horizontal surface, the velocity of the lowest point on the disc is always zero.

Assertion: A uniform cubical block (of side $a$) undergoes translational motion on a smooth horizontal surface under action of horizontal force $F$ as shown. Under the given condition, the horizontal surface exerts normal reaction non-uniformly on lower surface of the block.

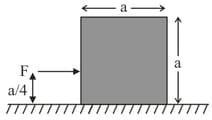
Reason: For the cubical block given in statement $1$, the horizontal force $F$ has tendency to rotate the cube about its centre in clockwise sense. Hence, the lower right edge of cube presses the horizontal surface harder in comparison to the force exerted by lower left edge of cube on horizontal surface.