A vinyl record is played by rotating the record so that an approximately circular groove in the vinyl slides under a stylus. Bumps in the groove run into the stylus, causing it to oscillate. The equipment converts those oscillations to electrical signals and then to sound. Suppose that a record turns at the rate of $33\frac{1}{3} \mathrm{rev} {\min }^{-1}$, the groove being played is at a radius of $10.0 \mathrm{cm}$ and the bumps in the groove are uniformly separated by $1.85 \mathrm{mm}$. At what rate (hits per second) do the bumps hit the stylus?

(a) What is the angular speed $\omega$ about the polar axis of a point on Earth's surface at latitude $40° \mathrm{N}$? (Earth rotates about that axis.) (b) What is the linear speed $v$ of the point? What are (c) $\omega$ and (d) $v$ for a point at the equator?

A seed is on a turntable rotating at $33\frac{1}{3} \mathrm{rev} {\min }^{-1}$, $6.0 \mathrm{cm}$ from the rotation axis. What are (a) the seed's acceleration and (b) the least coefficient of static friction to avoid slippage?

(c) If the turntable had undergone a constant angular acceleration from rest in $0.25 \mathrm{s}$, what is the least coefficient to avoid slippage?

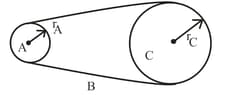
In the figure shown below, wheel $A$ of radius $r_{\mathrm{A}}=10 \mathrm{cm}$ is coupled by a belt $B$ to wheel $C$ of radius $r_{\mathrm{C}}=25 \mathrm{cm}$. The angular speed of wheel $A$ is increased from rest at a constant rate of $2.0 \mathrm{rad} {\mathrm{s}}^{-2}$. Find the time needed for the wheel $C$ to reach an angular speed of $100 \mathrm{rev} {\min }^{-1}$, assuming the belt does not slip. (Hint: If the belt does not slip, the linear speeds at the two rims must be equal.)

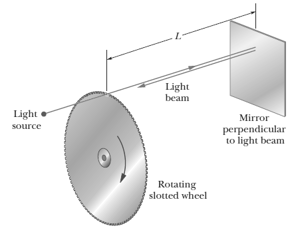
The below figure shows an early method of measuring the speed of light that makes use of a rotating slotted wheel. A beam of light passes through one of the slots at the outside edge of the wheel, travels to a distant mirror, and returns to the wheel just in time to pass through the next slot in the wheel. One such slotted wheel has a radius of $5.0 \mathrm{cm}$ and $500$  slots around its edge. Measurements taken when the mirror is $L=500 \mathrm{m}$ from the wheel indicate a speed of light of $3.0\times {10}^5 \mathrm{km} {\mathrm{s}}^{-1}$. $\left(a\right)$ What is the (constant) angular speed of the wheel? $\left(b\right)$ What is the linear speed of a point on the edge of the wheel?

A gyroscope flywheel of the radius $2.62 \mathrm{cm}$ is accelerated from rest at $14.2 \mathrm{rad} {\mathrm{s}}^{-2}$ until its angular speed is $2760 \mathrm{rev} {\min }^{-1}$.

$\left(a\right)$ What is the tangential acceleration of a point on the rim of the flywheel during this spin-up process?

$\left(b\right)$ What is the radial acceleration of this point when the flywheel is spinning at full speed?

$\left(c\right)$ Through what distance does a point on the rim move during the spin-up?