An initial momentum is imparted to a homogeneous cylinder as a result of which it begins to roll without slipping up an inclined plane at speed $v_0=4{ ms}^{-1}.$ The plane makes an angle of $30°$ with the horizontal. What time (in sec) does the cylinder take before stopping.

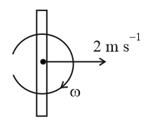
As shown in the figure, a rod moves with $v=2 \mathrm{m} {\mathrm{s}}^{-1}$ and rotates with $\omega =2\pi \mathrm{rad} {\mathrm{s}}^{-1}$. The point on the rod whose velocity is zero in this frame is at a distance $\frac{\beta }{\pi } \mathrm{m}$ below the centre of mass. Write the value of $\beta$.

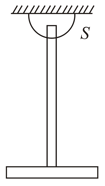
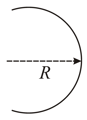
A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radius $R$ is placed horizontally at rest with its length parallel to the edge such that the axis of the cylinder and the edge of the block are in the same vertical plane as shown in figure. There is sufficient friction present at the edge, so that a very small displacement causes the cylinder to roll of the edge without slipping. Determine :

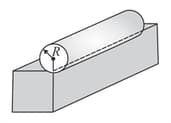
(i) The angle ${\mathrm{\theta }}_{\mathrm{C}}$ through which the cylinder rotates before it leaves contact with the edge.

(ii) The speed of the centre of mass of the cylinder before leaving contact with the edge and

(iii) The ratio of the translational to rotational kinetic energies of the cylinder when its centre of mass is in horizontal line with the edge.

A uniform rod of length $4\ell$ and mass $m$ is free to rotate about a horizontal axis passing through a point distance, $\ell$ from its one end. When the rod is horizontal, its angular velocity is $\omega$ as shown in figure. Calculate

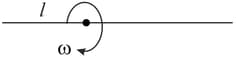
(i) reaction of axis at this instant,

(ii) acceleration of centre of mass of the rod at this instant,

(iii) reaction of axis and acceleration of centre of mass of the rod when rod becomes vertical for the first time.

(iv) minimum value of $\omega$ so that centre of rod can complete circular motion.

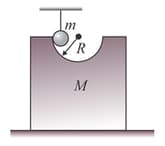
A semi circular track of radius $R=62.5\mathrm{cm}$ is cut in a block. Mass of block, having track, is $M=1\mathrm{kg}$ and rests over a smooth horizontal floor. A cylinder of radius $r=10 \mathrm{cm}$ and mass $m=0.5 \mathrm{kg}$ is hanging by thread such that axis of cylinder and track are in same level and surface of cylinder is in contact with the track as shown in figure. When the thread is burnt, cylinder starts to move down the track. Sufficient friction exists between surface of cylinder and track, so that cylinder does not slip. Calculate velocity of axis of cylinder and velocity of the block when it reaches bottom of the track. Also find force, applied by block on the floor at the moment. $\left(g=10 m{s}^{-2}\right)$

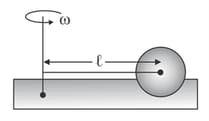
A thin rod is passing through the centre of a sphere. The rod is fixed to a vertical axis and the sphere is made to roll on a surface with friction. The radius of the sphere is $r,$ the mass is $m$ and the length of the rod is $l.$ The rod is rotating with an angular velocity ${\omega }_0.$ Find the energy of the sphere in terms of ${\omega }_0, m, l$ and $r.$ Assume the rod to be of negligible mass.