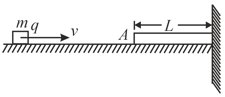
Figure shows a rod of length $L$ which is uniformly charged with linear charge density $\lambda$ kept on a smooth horizontal surface. Right end of rod is in contact with a vertical fixed wall. A block of mass m and charge q is projected with a velocity $v$ from a point very far from rod in the line of rod. Find the distance of the closest approach between the block & the left end $A$ of the rod.

A non-conducting disc of radius $a$ and uniform positive surface charge density $\sigma$ is placed on the ground with its axis vertical. A particle of mass $m$ and positive charge $q$ is dropped along the axis of the disc from a height $H$ with zero initial velocity. The particle has, $\frac{q}{m}=\frac{4{\epsilon }_{0}g}{ \sigma }$.

(i) Find the value of $H$ if the particle just reaches the disc.

(ii) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.

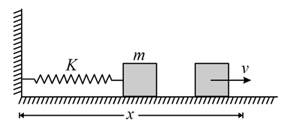
A block of mass $m$ is pushed against a spring of spring constant $k$ fixed at one end to a wall. The block can slide on a frictionless table as shown in the figure. The natural length of the spring is $L_0$ and it is compressed to one-fourth of the natural length and the block is released. Find its velocity as a function of its distance $\left(x\right)$ from the wall and the maximum velocity of the block. The block is not attached to the spring.

A block of mass $m$ rests on a rough horizontal plane having a coefficient of kinetic friction ${\mu }_k$ and coefficient of static friction ${\mu }_s$. The spring is in its natural length when a constant force of magnitude $P=\frac{5{\mu }_{k}mg}{4}$ acting on the block. The spring force $F$ is a function of extension $x \mathrm{as} F=k{x}^3$. (Where $k$ is spring constant)

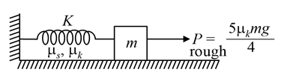
$\left(\mathrm{a}\right)$ Comment on the relation between ${\mu }_s$ and ${\mu }_k$ for the motion to start.

$\left(\mathrm{b}\right)$ Find the maximum extension in the spring. (Assume the force $P$ is sufficient to make the block move)

A particle of mass $m=1 \mathrm{kg}$ lying on $x$-axis experiences a force given by law $\overrightarrow{F}=x\left(3x–2\right)\hat{\mathrm{i}} \mathrm{N}$

where $x$ is the $x$-coordinate of the particle in meters.

$\left(\mathrm{a}\right)$ Locate the points on $x$-axis where the particle is in equilibrium.

$\left(\mathrm{b}\right)$ Draw the graph of variation of force $F$ ($y$-axis) with $x$-coordinate of the particle ($x$-axis). Hence or otherwise indicate at which positions the particle is in stable or unstable equilibrium.

$\left(\mathrm{c}\right)$ What is the minimum speed to be imparted to the particle placed at $x=4 \mathrm{meters}$ such that it reaches the origin.

A small bead of mass $m$ is free to slide on a fixed smooth vertical wire, as indicated in the diagram. One end of a light elastic string, of unstretched length $a$ and force constant $\frac{2mg}{a}$ is attached to $B$. The string passes through a smooth fixed ring $R$ and the other end of the string is attached to the fixed point $A$, $AR$ being horizontal. The point $O$ on the wire is at same horizontal level as $R$, and $AR=RO=a$.

(i) In the equilibrium position, find $OB$.

(ii) The bead $B$ is raised to a point $C$ of the wire above $O$, where $OC=a$, and is released from rest. Find the speed of the bead as it passes $O$, and find the greatest depth below $O$ of the bead in the subsequent motion. 

A particle of mass $m$ approaches a region of force starting from $r=+\infty .$ The potential energy function in terms of distance $r$ from the origin is given by,

$U\left(r\right)=\frac{K}{2a^3}\left(3a^2-r^2\right)$ for $0\le r\le a$

$=\frac{K}{r}$ for $r\ge a$  where $K>0$ (positive constant)

(a) Derive the force $F\mathit{ }\left(r\right)$ and determine whether it is repulsive or attractive.

(b) With what velocity should the particle start at $r=\infty$ to cross over to other side of the origin.

(c) If the velocity of the particle at $r=\infty$ is $\sqrt{\frac{2K}{am}}$ towards the origin describe the motion.