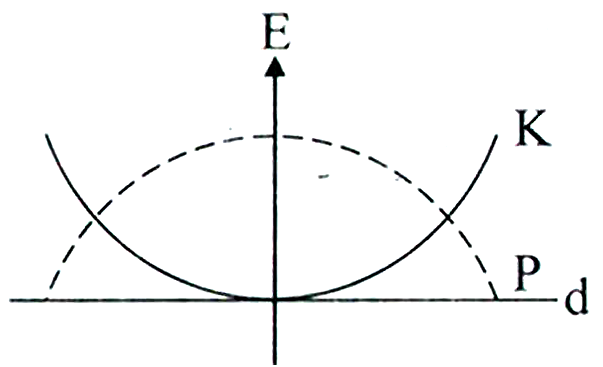
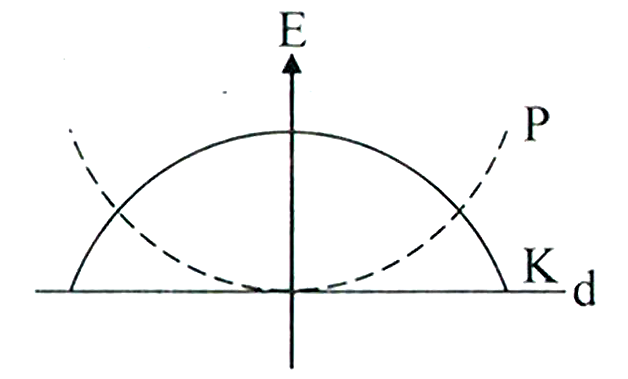
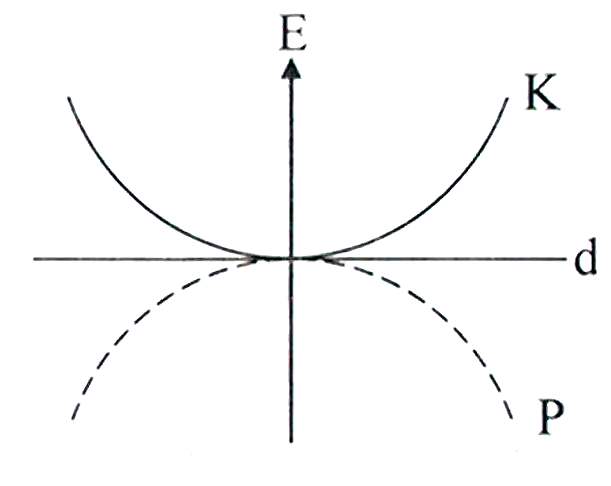
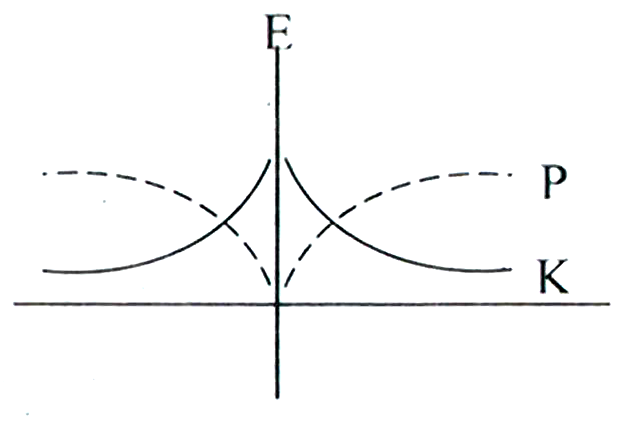
For a simple pendulum, a graph is plotted between its kinetic energy $\left(\mathrm{KE}\right)$ and potential energy $\left(\mathrm{PE}\right)$ against its displacement $d$. Which one of the following represents these correctly? (Graphs are schematic and not drawn to scale)

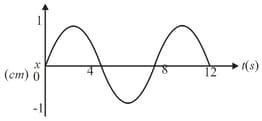
The $x-t$ graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at $t=\frac{4}{3} \mathrm{s}$ is

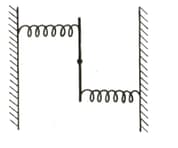
A uniform rod of length (L) and mass (M) is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $\left(\mathrm{k}\right)$ The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle (theta) in one direction and released. The frequency of oscillation is. ?

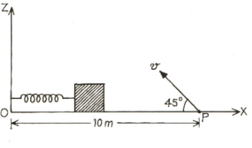
A small block is connected to one end of a massless spring of unstretched length $4.9 \mathrm{m}$. The other end of the spring is fixed as shown in the figure. The system lies on a horizontal frictionless surface. The block is stretched by $0.2 \mathrm{m}$  and released from rest at $\mathrm{t}=0$. lt then executes simple harmonic motion with angular frequency. $\mathrm{\omega }=\frac{\mathrm{\pi }}{3} \mathrm{rad}/\mathrm{s}$. Simultaneously at $\mathrm{t}=0$, a small pebble is projected with speed $\mathrm{v}$ from  point $\mathrm{P}$ at an angle of $45°$ as shown in the figure. Point P is at a horizontal distance of $10 \mathrm{m} \mathrm{from} \mathrm{O}$. If the pebble hits the block at $\mathrm{t}=1 \sec$, the value of $v$ is $:$
(take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ )

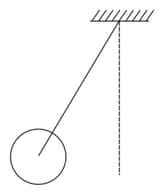
A metal rod of length $L$ and mass $m$ is pivoted at one end. A thin disk of mass $M$ and radius $R$ ($<L$) is attached at its centre to the free end of the rod. Consider two ways the disc is attached:

(Case $A$): The disc is not free to rotate about its centre and

(Case $B$): the disc is free to rotate about its centre.

The rod- disc system performs SHM in vertical plane after being released from the same displaced position. Which of the following statement(s) is (are) true?

A particle of mass $m$ is attached to one end of a massless spring of force constant$\mathrm{k}$, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time $\mathrm{t}=0$ with an initial velocity ${\mathrm{u}}_0$ when the speed of the particle is $0.5{\mathrm{u}}_0$ .It collides elastically with a rigid wall. After this collision.

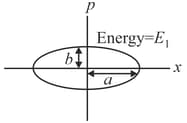
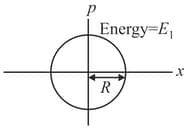
Two independent harmonic oscillators of equal masses oscillate about the origin with angular frequencies ${\mathrm{\omega }}_1$ and ${\mathrm{\omega }}_2$ and have total energies $E_1$ and $E_2$, respectively. The variations of their momenta $p$ with positions $x$ are shown in figures. If $\frac{a}{b}=n^2$ and $\frac{a}{R}=n$, then the correct equation(s) is (are),