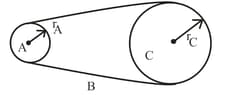
In the figure shown below, wheel $A$ of radius $r_{\mathrm{A}}=10 \mathrm{cm}$ is coupled by a belt $B$ to wheel $C$ of radius $r_{\mathrm{C}}=25 \mathrm{cm}$. The angular speed of wheel $A$ is increased from rest at a constant rate of $2.0 \mathrm{rad} {\mathrm{s}}^{-2}$. Find the time needed for the wheel $C$ to reach an angular speed of $100 \mathrm{rev} {\min }^{-1}$, assuming the belt does not slip. (Hint: If the belt does not slip, the linear speeds at the two rims must be equal.)

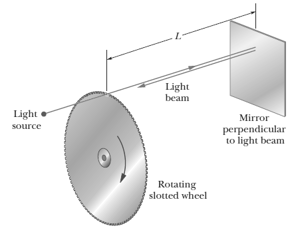
The below figure shows an early method of measuring the speed of light that makes use of a rotating slotted wheel. A beam of light passes through one of the slots at the outside edge of the wheel, travels to a distant mirror, and returns to the wheel just in time to pass through the next slot in the wheel. One such slotted wheel has a radius of $5.0 \mathrm{cm}$ and $500$  slots around its edge. Measurements taken when the mirror is $L=500 \mathrm{m}$ from the wheel indicate a speed of light of $3.0\times {10}^5 \mathrm{km} {\mathrm{s}}^{-1}$. $\left(a\right)$ What is the (constant) angular speed of the wheel? $\left(b\right)$ What is the linear speed of a point on the edge of the wheel?

A gyroscope flywheel of the radius $2.62 \mathrm{cm}$ is accelerated from rest at $14.2 \mathrm{rad} {\mathrm{s}}^{-2}$ until its angular speed is $2760 \mathrm{rev} {\min }^{-1}$.

$\left(a\right)$ What is the tangential acceleration of a point on the rim of the flywheel during this spin-up process?

$\left(b\right)$ What is the radial acceleration of this point when the flywheel is spinning at full speed?

$\left(c\right)$ Through what distance does a point on the rim move during the spin-up?

$\left(a\right)$ A uniform $2.00 \mathrm{kg}$ disk of radius $0.300 \mathrm{m}$ can rotate around its central axis like a merry-go-round. Beginning from rest at time $t=0$, it undergoes a constant angular acceleration of $30.0 \mathrm{rad} {\mathrm{s}}^{-2}$. When is the rotational kinetic energy equal to $2000 \mathrm{J}$?

$\left(b\right)$ Repeat the calculation but substitute a ring of the same mass and radius and assume that the spokes have negligible mass.

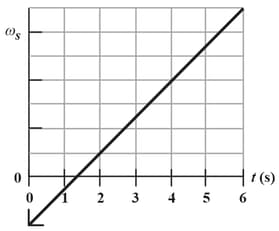
In the figure shown below gives angular speed versus time for a thin rod that rotates around one end. The scale on the $\omega$ axis is set by ${\omega }_s=6.0 \mathrm{rad} {\mathrm{s}}^{-1}$.
(a) What is the magnitude of the rod's angular acceleration?
(b) At $t=4.0 \mathrm{s}$, the rod has a rotational kinetic energy of $1.60 \mathrm{J}$. What is its kinetic energy at $t=0$?

A meter stick of negligible mass can rotate about a vertical axis through a point at distance $x$ from the point marked $0$. A small block of mass $0.100 \mathrm{kg}$ is glued at the mark of $0$, and a small block of mass $0.500 \mathrm{kg}$ is glued at the opposite end, at the mark of $1$. The stick and blocks are to rotate with an angular speed of $5.00 \mathrm{rad} {\min }^{-1}$.

$\left(a\right)$ For what choice of $x$ is the associated rotational kinetic energy least and

$\left(b\right)$ what is that least energy?

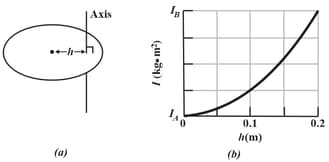
In the figure $\left(a\right)$ shown below, a disk that can rotate about an axis at a radial distance $h$ from the center of the disk. Figure $\left(b\right)$ gives the rotational inertia $I$ of the disk about the axis as a function of that distance $h$ from the centre out to the edge of the disk. The scale on the $I$ axis is set by $I_{\mathrm{A}}=0.050 \mathrm{kg} {\mathrm{m}}^2$ and $I_{\mathrm{B}}=0.150 \mathrm{kg} {\mathrm{m}}^2$. What is the mass of the disk?