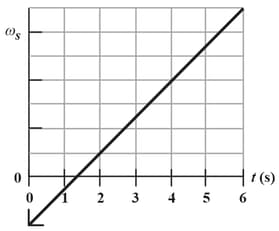
In the figure shown below gives angular speed versus time for a thin rod that rotates around one end. The scale on the $\omega$ axis is set by ${\omega }_s=6.0 \mathrm{rad} {\mathrm{s}}^{-1}$.
(a) What is the magnitude of the rod's angular acceleration?
(b) At $t=4.0 \mathrm{s}$, the rod has a rotational kinetic energy of $1.60 \mathrm{J}$. What is its kinetic energy at $t=0$?

A meter stick of negligible mass can rotate about a vertical axis through a point at distance $x$ from the point marked $0$. A small block of mass $0.100 \mathrm{kg}$ is glued at the mark of $0$, and a small block of mass $0.500 \mathrm{kg}$ is glued at the opposite end, at the mark of $1$. The stick and blocks are to rotate with an angular speed of $5.00 \mathrm{rad} {\min }^{-1}$.

$\left(a\right)$ For what choice of $x$ is the associated rotational kinetic energy least and

$\left(b\right)$ what is that least energy?

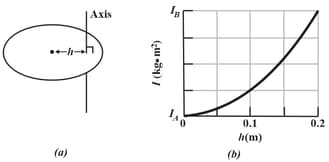
In the figure $\left(a\right)$ shown below, a disk that can rotate about an axis at a radial distance $h$ from the center of the disk. Figure $\left(b\right)$ gives the rotational inertia $I$ of the disk about the axis as a function of that distance $h$ from the centre out to the edge of the disk. The scale on the $I$ axis is set by $I_{\mathrm{A}}=0.050 \mathrm{kg} {\mathrm{m}}^2$ and $I_{\mathrm{B}}=0.150 \mathrm{kg} {\mathrm{m}}^2$. What is the mass of the disk?

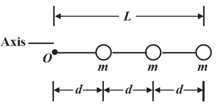
In the figure shown below three $0.0100 \mathrm{kg}$ particles that have been glued to a rod of length $L=8.00 \mathrm{cm}$ and negligible mass. The assembly can rotate around a perpendicular axis through point $O$ at the left end. If we remove one particle (that is, $33\%$ of the mass), by what percentage does the rotational inertia of the assembly around the rotation axis decrease when that removed particle is $\left(a\right)$ the innermost one and $\left(b\right)$ the outermost one?

In the given below figure shows an arrangement of $15$ Identical discs that have been glued together in a rod-like shape of length $L=1.0000 \mathrm{m}$, and (total) mass $M=100.0 \mathrm{mg}$. The discs are uniform, and the disc arrangement can rotate about a perpendicular axis through its central disc at point $O$.

$\left(a\right)$ What is the rotational inertia of the arrangement about that axis?

$\left(b\right)$ If we approximated the arrangement as being a uniform rod of mass $M$ and length $L$, what percentage error would we make in using the formula used to calculate the rotational inertia?

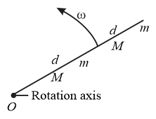
In the given below figure two particles, each with mass $m=0.85 \mathrm{kg}$, are fastened to each other, and to a rotation axis at $O$, by two thin rods, each with length $d=5.6 \mathrm{cm}$, and mass $M=1.2 \mathrm{kg}$. The combination rotates around the rotation axis with the angular speed $\mathrm{\omega }=0.30 \mathrm{rad} {\mathrm{s}}^{-1}$. Measured about $O$ what are the combination's $\left(a\right)$ rotational inertia and $\left(b\right)$ kinetic energy?

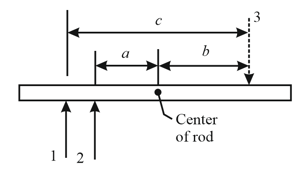
In the figure shown below, is an overhead view of a rod of length $1.0 \mathrm{m}$ and mass $1.0 \mathrm{kg}$ that is lying stationary on a frictionless surface when three bullets hit it simultaneously. The bullets move along paths that are in the plane of the rod and perpendicular to the rod. Bullet $1$ has mass $10 \mathrm{g}$ and speed $2.0 \mathrm{m} {\mathrm{s}}^{-1}$. Bullet $2$ has mass $20 \mathrm{g}$ has and speed $3.0 {\mathrm{ms}}^{-1}$. Bullet $3$ has mass $30 \mathrm{g}$ and speed $5.0 \mathrm{m} {\mathrm{s}}^{-1}$. The labelled distances are $a=10 \mathrm{cm}$, $b=60 \mathrm{cm}$ and $c=80 \mathrm{cm}.$ As a result of the impacts, the rod-bullets system rotates around its centre of mass while the centre of mass moves in a straight line over the frictionless surface. (a) What is the linear speed of the system's centre of mass?
(b) What is the distance between the rod's centre and the system's centre of mass?
(c) What is the rotational inertia of the system about the system's centre of mass?