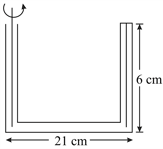
Length of horizontal arm of a uniform cross-section U-tube is $\ell =21 \mathrm{cm}$ and ends of both of the vertical arms are open to surrounding of pressure $10500 \mathrm{N} {\mathrm{m}}^{-2}$. A liquid of density $\rho ={10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$ is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed, and the tube is then rotated about a vertical axis passing through the other vertical arm with angular velocity ${\omega }_0=10 \mathrm{rad} s^{-1}.$ If length of each vertical arm be $a=6 \mathrm{cm}.$ Calculate the length of air column in the sealed arm : $\left[g=10 \mathrm{m} {\mathrm{s}}^{-2}\right]$

A ball of density d is dropped onto a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time t1. Next, the ball is released and it falls through the same height before striking the surface of a liquid of density${\mathrm{d}}_{\mathrm{L}}.$

$\left(\mathrm{a}\right)$ If $\mathrm{d} < {\mathrm{d}}_{\mathrm{L}},$ obtain an expression $(\mathrm{in} \mathrm{terms} \mathrm{of} \mathrm{d} , {\mathrm{t}}_1 \mathrm{and} {\mathrm{d}}_{\mathrm{L}})$ for the time ${\mathrm{t}}_2$ the ball takes to come back to the position from which it was released.

$\left(\mathrm{b}\right)$ Is the motion of the ball simple harmonic?

$\left(\mathrm{c}\right)$ If $\mathrm{d} = {\mathrm{d}}_{\mathrm{L}},$ how does the speed of the ball depend on its depth inside the liquid ?
     Neglect all frictional and other dissipative forces. Assume the depth of the liquid to be large.

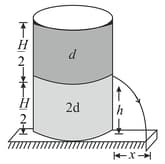
A container of large uniform cross-sectional area $A$ resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities $\mathrm{d}$ and $2\mathrm{d},$ each of height $\frac{H}{2}$ as shown in figure. The lower density liquid is open to the atmosphere having, pressure $P_{0^{\text{'}}}$

(i) A homogeneous solid cylinder of length $L\left(L<\frac{H}{2}\right),$ crosssectional area $\frac{A}{5}$ is immersed such that if floats with its axis vertical at the liquid-liquid interface with length $\frac{L}{4}$ in the denser liquid. Determine:
(a) the density $D$ of the solid,

(b) the total pressure at the bottom of the container.

(ii) The cylinder is removed and the original arrangement is restored. A tiny hole of area s $(s<<A)$ is, punched on the vertical side of the container at a height $h\left(h<\frac{H}{2}\right).$ Determine:
(a) the initial speed of efflux of the liquid at the hole

(b) the horizontal distance $\mathrm{x}$ travelled by the liquid initially, and

(c) the height $h_m$ at which the hole should be punched so that the liquid travels the maximum distance) $x_m$ initially. Also calculate ${\mathrm{x}}_{\mathrm{m}}.$ (Neglect the air resistance in these calculations)

An open rectangular tank of dimension $5 \mathrm{m}\times 4 \mathrm{m}\times 3 \mathrm{m}$ containing water upto a height of $2 \mathrm{m}$ is accelerated horizontally along the longer side.

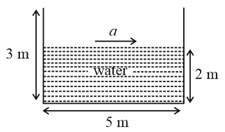
(i) Determine the maximum acceleration that can be given without spilling the water.

(ii) Calculate the percentage of water split over, if this acceleration is increased by $20\%.$

(iii) If initially, the tank is closed at the top and is accelerated horizontally by $9 \mathrm{m} {\mathrm{s}}^{-2},$ find the gauge pressure at the bottom of the front and rear walls of the tank.

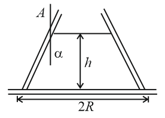
A conical vessel without a bottom stands on a table. A liquid is poured with the vessel & as the level reaches $h$, the pressure of the liquid raises the vessel. The radius of the base of the vessel is $R$ and half angle of the cone is $\alpha$ and the weight of the vessel is $W.$ What is the density of the liquid?

A cylindrical tank having cross-sectional area $A=0.5{ \mathrm{m}}^2$ is filled with two liquids of densities ${\rho }_1=900 \mathrm{kg} {\mathrm{m}}^{-3}$ and ${\rho }_2=600 \mathrm{kg} {\mathrm{m}}^{-3},$ to a height $h=60 \mathrm{cm}$ as shown in the figure. A small hole having area $a=5{ \mathrm{cm}}^2$ is made in right vertical wall at a height $y=20 \mathrm{cm}$ from the bottom. Calculate

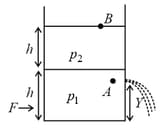
(i) velocity of efflux.

(ii) horizontal force $F$ to keep the cylinder in static equilibrium, if it is placed on a smooth horizontal plane

(iii) Minimum and maximum value of $F$ to keep the cylinder at rest. The coefficient of friction between cylinder and the plane is $\mu =0.1$

(iv) velocity of the top most layer of the liquid column and also the velocity of the boundary separating the two liquids.

A cylindrical wooden float whose base area $S=4000{ \mathrm{cm}}^2$ and the altitude $H=50 \mathrm{cm}$ drifts on the water surface. Specific weight of wood $d=0.8 \mathrm{gf} {\mathrm{cm}}^{-3}.$

$\left(\mathrm{i}\right)$ What work must be performed to take the float out of the water?

$\left(\mathrm{ii}\right)$ Compute the work to be performed to submerged completely the float into the water.