Let $B$ and $E$ denote induction of magnetic field and energy density at mid-point of a long solenoid carrying a current. The graph between $E$ and $B$ will be,

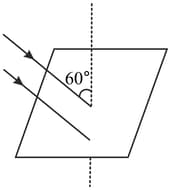
A square Ioop of side $4 \mathrm{cm}$ is lying on a horizontal table. A uniform magnetic field of $0.5 \mathrm{T}$ is directed downwards at an angle of $60°$ with vertical as shown in the figure. If the field increases from zero to its final value in $0.2 \mathrm{s}$, the e.m.f. induced in loop will be,

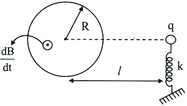
There is horizontal cylindrical uniform but time-varying magnetic field increasing at a constant rate $\frac{\mathrm{d}B}{\mathrm{d}t}$ as shown. A charged particle having charge $q$ and mass $m$ kept in equilibrium at the top of a spring of spring constant $k$ in such a way that it is on the horizontal line passing through the centre of the magnetic field as shown in figure. The compression in the spring will be,

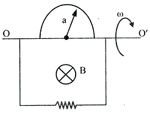
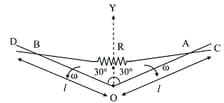
If the figure, there exists uniform magnetic field $B$ directed into the plane of paper. The wire $C$$D$ is in the shape of an arc and is fixed. $OA$ and $OB$ are the wires rotating with angular velocity $\omega$ as shown in figure in same plane as that of arc $OA=OB=l$ and each wire makes angle, $\theta =30°$ with $Y\text{-axis}$, the current through resistance $R$ is (wires $OA$ and $OB$ have no resistance),

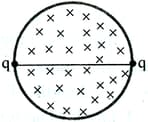
A cylindrical region of uniform magnetic field exists perpendicular to plane of paper which is increasing at a constant rate $\frac{\mathrm{d}B}{\mathrm{d}t}=\alpha$. The diameter of cylindrical region is $l$. A non-conducting rigid rod of length $l$ having two charged particles is kept fixed on the diameter of cylindrical region w.r.t. inertial frame. If two charged particles, having charges $\overline{q}$ each, is kept fixed at the ends of non-conducting rod, the net force on any one of the charge is,

A wire shaped as a semi-circle of radius $a$ rotates about an axis ${\mathrm{OO}}^{\text{'}}$ with an angular velocity $\omega$ in a uniform magnetic field of induction $B$ (shown in figure). The axis of rotation is perpendicular to the field direction. The total resistance of the circuit is equal to $R$. Neglecting the magnetic field of induced current, calculate the mean amount of thermal power being generated in the loop during one rotation period and express it in the form:
$P_{\text{mean}}=B^{\mathrm{m}}{a}^{\mathrm{n}}{\omega }^{\mathrm{p}}\times$ constant. Find the value of $P$.