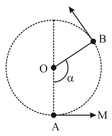
On a banked race track, while the largest path has a radius of $175 \mathrm{m}$, the smallest circular path on which cars can move has a radius of $111 \mathrm{m}$ as the drawing illustrates. The height of the outer wall is $16 \mathrm{m}$.

(a) the smallest and

(b) the largest speed at which cars can move on this track without relying on friction.

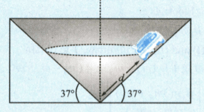
A racetrack has the shape of an inverted cone as the drawing shows. On this surface, the cars race in circles that are parallel to the ground. For a speed of $34.0 \mathrm{m} {\mathrm{s}}^{-1}$, at what value of the distance $d$ should a driver locate his car if he wishes to stay on a circular path without depending on friction?

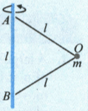
A particle of mass $m$ is connected with two inextensible strings $AO$ and $BO$ of equal a lengths $l$. These two strings are finally attached to a vertical rod at points $A$ and $B$ as shown in figure. Distance between $A$ and $B$ is also $l$. The setup is rotated with constant angular speed $\omega$ with rod as the axis.

(a) Find the values of $\omega$ for which the particle remains at point $B$.

(b) Find the range of values of $\omega$ for which tension $\left(T_1\right)$ in the string $AO$ is greater than $mg$ but the other string remains slack.

(C) Find the value of $\omega$ for which tension $\left(T_1\right)$ in string $AO$ is twice the tension $\left(T_2\right)$ in the string $BO$.

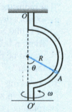
A sleeve $A$ can slide freely along a smooth rod bent in the shape of a half circle of radius $R$. The system is set in rotation with a constant angular velocity $\omega$ about a vertical axis $OO\text{'}$. Find the angle $\mathrm{\theta }$ corresponding to the steady position of the sleeve.

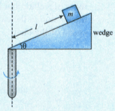
A small wedge whose base is horizontal is fixed to a vertical rod as shown in the figure. The sloping side of the wedge is frictionless and the wedge is spun with a constant angular speed $\omega$ about vertical axis as shown in the figure. Find

(a) the value of angular speed $\omega$ for which the block of mass $m$ just does not slide down the wedge, 

(b) the normal reaction on the block by wedge when block does not slip relative to wedge.

The bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity $u=\sqrt{3gl}$, where $l$ is the length of the pendulum. Find the angle rotated by the string before it becomes slack.