MEDIUM
JEE Advanced
IMPORTANT
Earn 100
One mole of an ideal monatomic gas undergoes an adiabatic expansion in which its volume becomes eight times its initial value. If the initial temperature of the gas is and the universal gas constant , then how much is the decrease in its internal energy (in ) ?
71.01% studentsanswered this correctly

Important Questions on Thermodynamics
HARD
JEE Advanced
IMPORTANT
A gas is enclosed in a cylinder with a movable frictionless piston. Its initial thermodynamic state at pressure changes to a final state at in an adiabatic quasi-static process, such that constant. Consider another thermodynamic process that brings the system from the same initial state to the same final state in two steps: an isobaric expansion at followed by an isochoric (isovolumetric) process at volumes . The amount of heat supplied to the system in the two step process is approximately
HARD
JEE Advanced
IMPORTANT
An ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature , pressure and volume and the spring is in its relaxed state. The gas is then heated very slowly to temperature , pressure and volume . During this process the piston moves out by a distance . Ignoring the friction between the piston the cylinder, the correct statement(s) is (are)
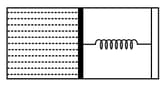
HARD
JEE Advanced
IMPORTANT
Consider one mole of helium gas enclosed in a container at initial pressure and volume . It expands isothermally to volume . After this, the gas expands adiabatically and its volume becomes . The work done by the gas during isothermal and adiabatic expansion processes are and , then is _________ .
HARD
JEE Advanced
IMPORTANT
One mole of a monoatomic ideal gas goes through a thermodynamic cycle, as shown in the volume versus temperature diagram. The correct statement(s) is/are:
[ is the gas constant]
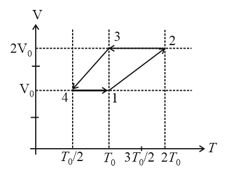
HARD
JEE Advanced
IMPORTANT
One mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true?
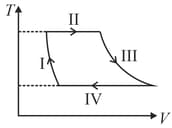
HARD
JEE Advanced
IMPORTANT
An ideal gas is undergoing a cyclic thermodynamic process in different ways as shown in the corresponding P-V diagrams in column 3 of the table. Consider only the path from state to state . denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic process. Here is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is .
| Column – 1 | Column – 2 | Column – 3 |
| (I) | (i) Isothermal | (P) 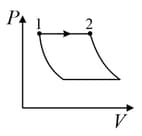 |
| (II) | (ii) Isochoric | (Q) 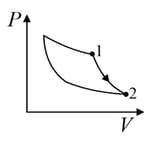 |
| (III) | (iii) Isobaric | (R) 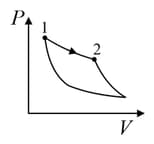 |
| (IV) | (iv) Adiabatic | (S) 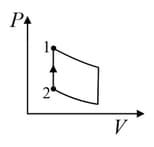 |
HARD
JEE Advanced
IMPORTANT
An ideal gas is undergoing a cyclic thermodynamic process in different ways as shown in the corresponding P-V diagrams in column 3 of the table. Consider only the path from state 1 to state 2. W denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic process. Here is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is .
| Column – 1 | Column – 2 | Column – 3 |
| (I) | (i) Isothermal | (P) 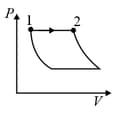 |
| (II) | (ii) Isochoric | (Q) 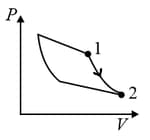 |
| (III) | (iii) Isobaric | (R) 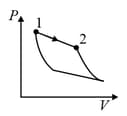 |
| (IV) | (iv) Adiabatic | (S) 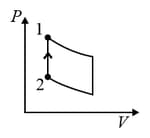 |
HARD
JEE Advanced
IMPORTANT
An ideal gas is undergoing a cyclic thermodynamic process in different ways as shown in the corresponding P-V diagrams in column 3 of the table. Consider only the path from state 1 to state 2. W denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic process. Here is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is n.
| Column – 1 | Column – 2 | Column – 3 |
| (I) | (i) Isothermal | (P) 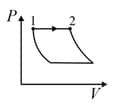 |
| (II) | (ii) Isochoric | (Q) 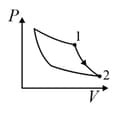 |
| (III) | (iii) Isobaric | (R) 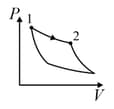 |
| (IV) | (iv) Adiabatic | (S) 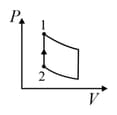 |
