Protons and helium nuclei from the Sun pass into the Earth's atmosphere above the poles, where the magnetic flux density is $6.0\times {10}^{-5}T.$ The particles are moving at a speed of $1.0\times {10}^{6}m{s}^{-1}$ at right angles to the magnetic field in this region. The magnetic field can be assumed to be uniform.

(a) Calculate the radius of the path of a proton as it passes above the Earth's pole.

Mass of a helium nucleus $=6.8\times {10}^{-27} kg$
Charge on a helium nucleus$=3.2\times {10}^{-19}C$

Mass of proton $=1.67\times {10}^{-27 }kg$

Charge on proton $=1.6\times {10}^{-19} C$

Protons and helium nuclei from the Sun pass into the Earth's atmosphere above the poles, where the magnetic flux density is$6.0\times {10}^{-5}T.$ The particles are moving at a speed of $1.0\times {10}^{6}m{s}^{-1}$ at right angles to the magnetic field in this region. The magnetic field can be assumed to be uniform.

(b) Sketch a diagram to show the deflection caused by the magnetic field to the paths of a proton and of a helium nucleus that both have the same initial velocity as they enter the magnetic field.

This diagram shows a thin slice of metal of thickness $t$ and width $d$. The metal slice is in a magnetic field of flux density $B$ and carries a current $I$, as shown.

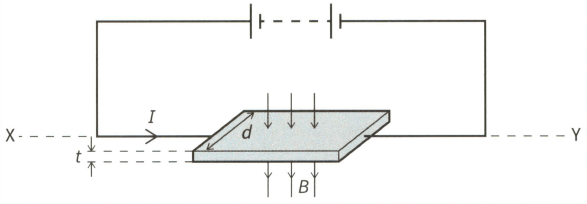
Copy the diagram and mark the slice that becomes negative because of the Hall effect.

This diagram shows a thin slice of metal of thickness $t$ and width $d$. The metal slice is in a magnetic field of flux density $B$ and carries a current $I$, as shown.

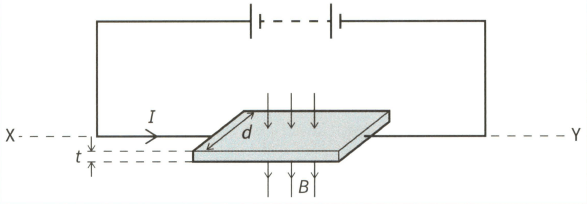
Copy the diagram and mark where a voltmeter needs to be placed to measure the Hall voltage.
 

This diagram shows a thin slice of metal of thickness $t$ and width $d$. The metal slice is in a magnetic field of flux density $B$ and carries a current $I$, as shown.

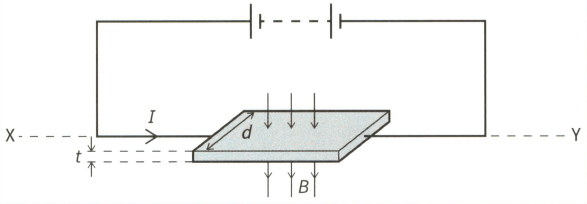
Derive an expression for the Hall voltage in terms of $I, B, t,$ the number density of the charge carriers $n$ in the metal and the charge on an electric iron.
 

This diagram shows a thin slice of metal of thickness $t$ and width $d$. The metal slice is in a magnetic field of flux density $B$ and carries a current $I$, as shown.

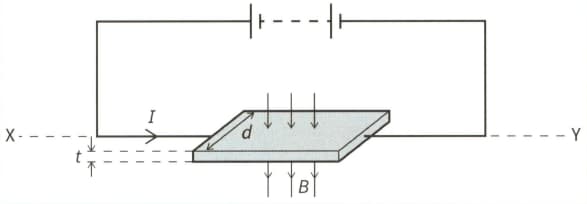
Given that $I=40 rnA, d=9.0 mm, t=0.030 mm, B=0.60T,$ $e=1.6\times {10}^{-19} C \text{and} n=8.5\times {10}^{28} m^{-3}, \text{calculate}$ theme an drift velocity v of the free electrons in the metal.

This diagram shows a thin slice of metal of thickness $t$ and width $d$. The metal slice is in a magnetic field of flux density $B$ and carries a current $I$, as shown.

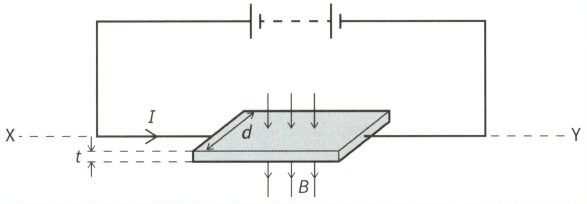
Given that $I=40 rnA, d=9.0 mm, t=0.030 mm, B=0.60T,$ $e=1.6\times {10}^{-19} C \text{and} n=8.5\times {10}^{28} m^{-3}, \text{calculate}$ the Hall voltage across the metal slice. 

This diagram shows a thin slice of metal of thickness $t$ and width $d$. The metal slice is in a magnetic field of flux density $B$ and carries a current $I$, as shown.

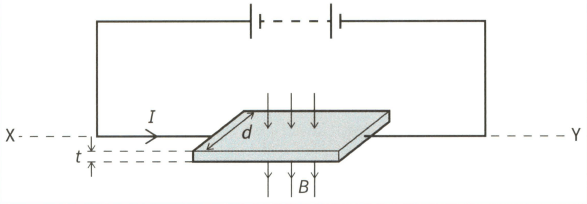
(c) Given that $I=40 mA, d=9.0 mm, t=0.030 mm, B=0.60T,$

Calculate the percentage uncertainty in the mean drift velocity v of the electrons, assuming the percentage uncertainties in the quantities are as shown.

This diagram shows a thin slice of metal of thickness $t$ and width $d$. The metal slice is in a magnetic field of flux density $B$ and carries a current $I$, as shown.

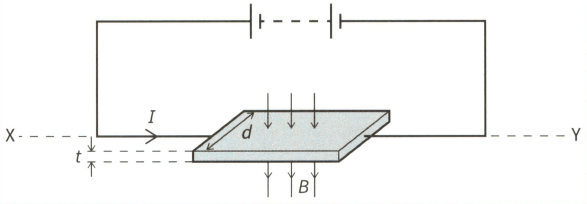
Explain why, in terms of the movement of electrons, the Hall voltage increases when I increase.