Sofia has made this pattern from yellow and blue tiles. She also has two spare blue tiles.

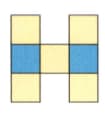
There are eight different ways I can add the two blue tiles to the pattern to make a pattern with one line of symmetry.

There are two different ways I can add the two blue tiles to the pattern to make a pattern with two lines of symmetry.

There is only one way I can add the two blue tiles to the pattern to make a pattern with four lines of symmetry.

Show that Sofia's statement are correct. You may join the tiles either side to side  or corner to corner .

Song has five blue tiles and four white tiles.

Draw two different ways that Song could arrange these tiles so that he has a shape with an order of rotational symmetry of $4$.

Song has five blue tiles and four white tiles.

Draw two different ways that Song could arrange these tiles so that he has a shape with an order of rotational symmetry of $4$. For each of the patterns you drew, how many lines of symmetry do your patterns of tiles have.

For the diagram shown, write down the letters of the lines that are tangent to the circle.

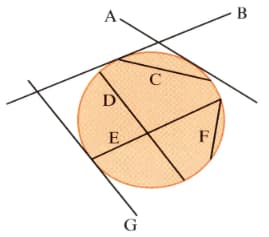
For the diagram shown, write down the letters of the lines that are chords of the circle.

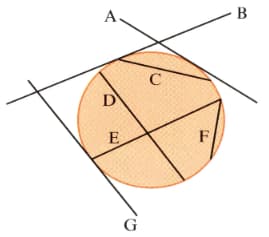
This is part of Omar's homework.

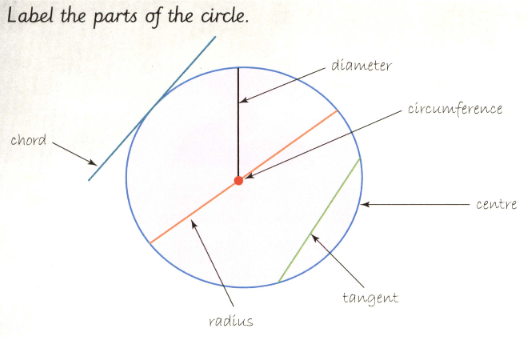
Omar has made a lot of mistakes. Copy the diagram and correctly label the parts of the circle.

Marcus draws this diagram.

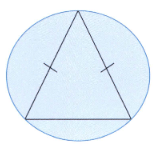
I can draw three chords inside a circle that makes an isosceles triangle.

Now inside the circle draw three chords that make a scalene triangle.

Marcus draws this diagram.

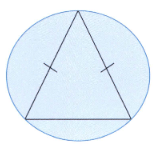
I can draw three chords inside a circle that makes an isosceles triangle.

Now inside the circle draw four chords that make a rectangle.

Zara draws this diagram.

 
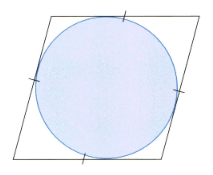
I can draw four tangents to the circle to make a rhombus.

I know it is a rhombus because it has:

Two pairs of parallel sides

Four sides of equal length

Opposite angles are equal

Two lines of symmetry.

Draw a circle. Draw four tangents to the circle to make a square.