Suggest how the Hall effect could be used to determine the number density of charge carriers n in a semiconducting material.

A scientist is doing an experiment on a beam of electrons travelling at right angles to a uniform magnetic field of flux density $B$. The graph shows the variation of the magnetic force $F$ acting on an electron with the speed v of the electron.

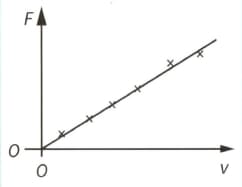
The gradient of the graph is $G$. The magnitude of the charge on the electron is e. What is the correct relationship for the magnetic flux density $B$?

A $B=G$, B $B=G\times e$, C $B=\frac{G}{e}$, D $B=\frac{e}{G}$

An electron beam is produced from an electron gun in which each electron is accelerated through a potential difference ($p.d.$) of $1.6 kV.$ When these electrons pass at right angles through a magnetic field of flux density $8.0 mT,$, the radius of curvature of the electron beam is $0.017 m$

Calculate the ratio $\frac{e}{m_e}$(known as the specific charge of the electron).

Two particles, an $\alpha$-particle and a $\beta$-particle, are travelling through a uniform magnetic field. They have the same speed and their velocities are at right angles to the field. Determine the ratio of:

(a) the mass of the $\alpha$-particle to the mass of the $\beta$-particle.

Mass of proton $m=1.67\times {10}^{-27 }kg$

Two particles, an $\alpha -$particle and a $\beta -$particle, are travelling through a uniform magnetic field. They have the same speed and their velocities are at right angles to the field. Determine the ratio of:

(b) the charge of the $\alpha -$particle to the charge of the$\beta -$particle.

Two particles, an $\alpha$-particle and a $\beta$-particle, are travelling through a uniform magnetic field. They have the same speed and their velocities are at right angles to the field. Determine the ratio of:

(c) the force on the $\alpha$-particle to the force on the $\beta$-particle

Two particles, an $\alpha$-particle and a $\beta$-particle, are travelling through a uniform magnetic field. They have the same speed and their velocities are at right angles to the field. Determine the ratio of:

(d) the radius of the $\alpha$-particle's orbit to the radius of the $\beta$-particle's orbit.