Suppose the particle of the previous problem has a mass and a speed before the collision and it sticks to the rod after the collision. The rod has a mass .
(a) Find the velocity of the centre of mass of the system constituting "the rod plus the particle".
(b) Find the velocity of the particle with respect to before the collision.
(c) Find the velocity of the rod with respect to before the collision.
(d) Find the angular momentum of the particle and of the rod about the centre of mass before the collision.
(e) Find the moment of inertia of the system about the vertical axis through the centre of mass after the collision.
(f) Find the velocity of the centre of mass and the angular velocity of the system about the centre of mass after the collision.

Important Questions on Rotational Mechanics
Two small balls and each of mass are joined rigidly to the ends of a light rod of length in the figure. The system translates on a frictionless horizontal surface with a velocity in a direction perpendicular to the rod. A particle of mass kept at rest on the surface sticks to the ball as the ball collides with it. Find
(a) the linear speeds of the balls and after the collision.
(b) the velocity of the centre of mass of the system .
(c) the angular speed of the system about after the collision.
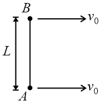
(Hint: The light rod will exert a force on the ball only along its length).
Suppose the rod with the balls and of the previous problem is clamped at the centre in such a way that it can rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle of the same mass is dropped from a height on the ball . The particle collides with and sticks to it.
(a) Find the angular momentum and the angular speed of the system just after the collision.
(b) What should be the minimum value of , so that the system makes a full rotation after the collision.
Previous problem:

Two blocks of masses and are connected through a light string going over a pulley, is free to rotate about its axis. The pulley has a moment of inertia and a radius of . Find
the kinetic energy of the system as the block falls through ,
the speed of the blocks at this instant.
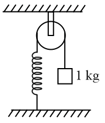
The pulley shown in figure. It has a radius of and moment of inertia . The string goes over, is attached to one end of a vertical spring of spring constant fixed from below and supports a of mass at the other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has descended through . Take ().
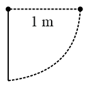
A meter stick weighing is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end (shown in the figure). A particle of mass is attached to the upper end of the stick through a light string of length . Initially, the rod is kept vertical and the string horizontal when the system is released from rest. The particle collides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.