Students in an after-school activity programme register for either trampolining or table tennis. The table shows students' choices by gender: Trampolining Table tennis Total Male 39 16 55 Female 21 14 35 A student is selected at random from the group. Find: P (male trampoliner)

The following table shows students choices by gender Trampolining Table tennis Total Male 39 16 55 Female 21 14 35 We need to find the probability that the selected student is a male and registered for trampoliner. Now, the Probability of the selected student is a male and registered for trampoliner. = Number of male students selecting trampoliner Total number of trampoliner choosing students = 39 21 + 39 = 39 60 = 13 20 Hence, the required probability is 13 20 .

Students in an after-school activity programme register for either trampolining or table tennis. The table shows students' choices by gender: Trampolining Table tennis Total Male 39 16 55 Female 21 14 35 A student is selected at random from the group. Find: P (trampoliner)

The following table shows students choices by gender Trampolining Table tennis Total Male 39 16 55 Female 21 14 35 We need to find the probability that the selected student is the one who chose trampoliner. Now, the Probability that the selected student has chosen trampoliner = Number of students chosen trampoliner Total number of students registered = 39 + 21 55 + 35 = 60 90 = 2 3 Hence, the required probability is 2 3 .

Students in an after-school activity programme register for either trampolining or table tennis. The table shows students' choices by gender: Trampolining Table tennis Total Male 39 16 55 Female 21 14 35 A student is selected at random from the group. Find: P (female)

The following table shows students choices by gender Trampolining Table tennis Total Male 39 16 55 Female 21 14 35 We need to find the probability of selected student being a female. Now, the Probability that the selected student is a female = Number of female students Total number of students registered = 21 + 14 55 + 35 = 35 90 = 7 18 Hence, the required probability is 7 18 .

Students in an after-school activity programme register for either trampolining or table tennis. The table shows students' choices by gender: Trampolining Table tennis Total Male 39 16 55 Female 21 14 35 A student is selected at random from the group. Determine whether or not the events trampolining and table tennis are independent events.

The following table shows students choices by gender Trampolining Table tennis Total Male 39 16 55 Female 21 14 35 Let E be the event that a student selected has chosen Trampolining and F be the event that a student selected has chosen Table tennis. Now, Probability of occurrence of event E = P E = 39 + 21 55 + 35 = 60 90 = 2 3 Probability of occurrence of event F = P F = 16 + 14 55 + 35 = 30 90 = 1 3 Now, since the number of students choosing both Trampolining and Table tennis = n E ∩ F = 0 ⇒ P E ∩ F = 0 Thus, we can say that P E × P F = 2 3 × 1 3 = 2 9 ≠ P E ∩ F Hence, the events E and F are not an independent events.

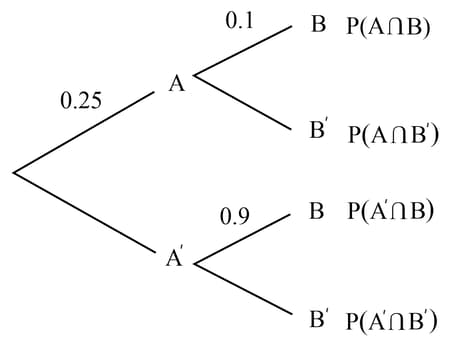
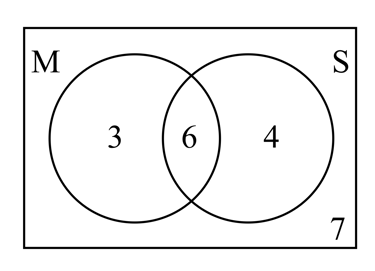
The Venn diagram shows the number of students in a class taking Mathematics Mand Science S Use it to determine whether or not taking Mathematics and Science are independent events

MEDIUM

MYP:4-5

IMPORTANT

Extended MYP Mathematics A Concept based approach Years 4 & 5>Chapter 5 - Independent Events and Conditional Probability>Practice 1>Q 5

In a different class, four students take Mathematics only, two take both Mathematics and Science, six take Science only and $12$ take neither subject. Determine whether the choice of taking Mathematics and taking Science ar independent events for this class.

EASY

MYP:4-5

IMPORTANT

Extended MYP Mathematics A Concept based approach Years 4 & 5>Chapter 5 - Independent Events and Conditional Probability>Practice 1>Q 6

Students in an after-school activity programme register for either trampolining or table tennis. The table shows students' choices by gender:

	Trampolining	Table tennis	Total
Male	39	16	55
Female	21	14	35

A student is selected at random from the group. Find: $P (male trampoliner)$

EASY

MYP:4-5

IMPORTANT

Extended MYP Mathematics A Concept based approach Years 4 & 5>Chapter 5 - Independent Events and Conditional Probability>Practice 1>Q 6

Students in an after-school activity programme register for either trampolining or table tennis. The table shows students' choices by gender:

	Trampolining	Table tennis	Total
Male	39	16	55
Female	21	14	35

A student is selected at random from the group. Find: $P (trampoliner)$

EASY

MYP:4-5

IMPORTANT

Extended MYP Mathematics A Concept based approach Years 4 & 5>Chapter 5 - Independent Events and Conditional Probability>Practice 1>Q 6

Students in an after-school activity programme register for either trampolining or table tennis. The table shows students' choices by gender:

	Trampolining	Table tennis	Total
Male	39	16	55
Female	21	14	35

A student is selected at random from the group. Find: $P (female)$

EASY

MYP:4-5

IMPORTANT

Extended MYP Mathematics A Concept based approach Years 4 & 5>Chapter 5 - Independent Events and Conditional Probability>Practice 1>Q 6

Students in an after-school activity programme register for either trampolining or table tennis. The table shows students' choices by gender:

	Trampolining	Table tennis	Total
Male	39	16	55
Female	21	14	35

A student is selected at random from the group. Determine whether or not the events trampolining and table tennis are independent events.

HARD

MYP:4-5

IMPORTANT

Extended MYP Mathematics A Concept based approach Years 4 & 5>Chapter 5 - Independent Events and Conditional Probability>Exploration 2>Q 1

The probability that it will rain tomorrow is $0.25$ . If it rains tomorrow, the probability that Amanda plays tennis is $0.1$ . If it doesn't rain tomorrow, the probability that she plays tennis is $0.9$ . Let $A$ be the event 'rains tomorrow' and $B$ be the event 'plays tennis'. Complete the following tree diagram for the events $A and B$ .

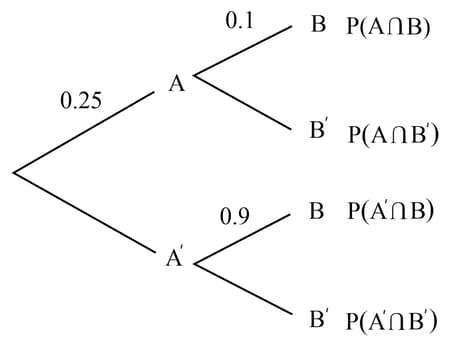
Question Image

HARD

MYP:4-5

IMPORTANT

Extended MYP Mathematics A Concept based approach Years 4 & 5>Chapter 5 - Independent Events and Conditional Probability>Exploration 2>Q 2

The probability that it will rain tomorrow is $0.25$ . If it rains tomorrow, the probability that Amanda plays tennis is $0.1$ . If it doesn't rain tomorrow, the probability that she plays tennis is $0.9$ . Let $A$ be the event 'rains tomorrow' and $B$ be the event 'plays tennis'. Complete the following tree diagram for the events $A and B$ . State whether $A and B$ are independent events or not.

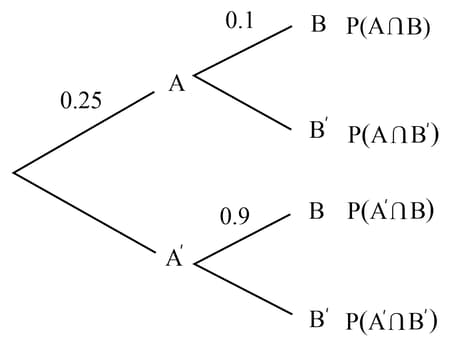
Question Image

HARD

MYP:4-5

IMPORTANT

Extended MYP Mathematics A Concept based approach Years 4 & 5>Chapter 5 - Independent Events and Conditional Probability>Exploration 2>Q 3

The probability that it will rain tomorrow is $0.25$ . If it rains tomorrow, the probability that Amanda plays tennis is $0.1$ . If it doesn't rain tomorrow, the probability that she plays tennis is $0.9$ . Let $A$ be the event 'rains tomorrow' and $B$ be the event 'plays tennis'. Complete the following tree diagram for the events $A and B$ . Find the probability that, Amanda plays tennis tomorrow, given that it will be raining

Question Image

The Venn diagram shows the number of students in a class taking Mathematics $M$ and Science $S$ . Use it to determine whether or not taking Mathematics and Science are independent events.

Important Questions on Independent Events and Conditional Probability

Learn and Prepare for any exam you want !

The Venn diagram shows the number of students in a class taking Mathematics M and Science S. Use it to determine whether or not taking Mathematics and Science are independent events.

Important Questions on Independent Events and Conditional Probability

Learn and Prepare for any exam you want !

The Venn diagram shows the number of students in a class taking Mathematics $M$ and Science $S$ . Use it to determine whether or not taking Mathematics and Science are independent events.