The area of a rhombus is $216$ square centimetres and the length of one of its diagonals is $24 \mathrm{centimetres}.$ Compute the following measurements of this rhombus.

The distance between sides is $k \mathrm{cm}$. Find the value of $k$.

A $68 \mathrm{centimetre}$ long rope is used to make a rhombus on the ground. The distance between pair of opposite corners is $16$ $\mathrm{centimetres}$. The distance between the other two corners is $k \mathrm{cm}$. Find the value of $k$.

Note: In textbook, the distance between a pair of opposite corners is given in metres but that should be in centimetres.

A $68 \mathrm{centimetre}$ long rope is used to make a rhombus on the ground. The distance between pair of opposite corners is $16 \mathrm{centimetres}$. The area of the ground bounded by the rope is $k {\mathrm{cm}}^2$. Find the value of $k$.

In the figure, the midpoints of the diagonals of a rhombus are joined to form a small quadrilateral:

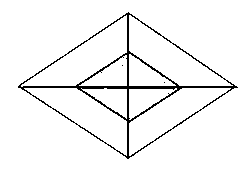
Prove that this quadrilateral is a rhombus.

In the figure, the midpoints of the diagonals of a rhombus are joined to form a small quadrilateral:

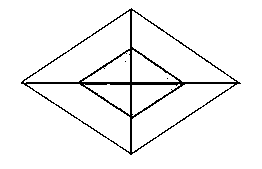
The area of the small rhombus is $3 \mathrm{square} \mathrm{centimetres}$. The area of the large rhombus is $\mathrm{k} {\mathrm{cm}}^2$. Find the value of $k$.

The area of the largest rhombus that can be drawn inside a rectangle of sides $6$ centimetres and $4$ centimetres is $\mathrm{K} {\mathrm{cm}}^2$. Find the value of $\mathrm{K}$.

Draw a rectangle of sides $7 \mathrm{centimetres}$ and $4 \mathrm{centimetres}$. Draw isosceles trapezium of the same area, with the following specifications.

Lengths of parallel sides $9 \mathrm{centimetres}$, $5 \mathrm{centimetres}$.

Draw a rectangle of sides $7 \mathrm{centimetres}$ and $4 \mathrm{centimetres}$. Draw isosceles trapezium of the same area, with the following specifications.

Lengths of non-parallel sides $5 \mathrm{centimetres}$.

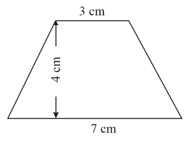
The area of the isosceles trapezium drawn below is $\mathrm{K} {\mathrm{cm}}^2$. Find the value for $\mathrm{K}$.